11 Trigonometrische Funktionen

Zum Test

11.1 Theorie

11.1.1 Winkeleinheiten

Ein Winkel kann durch den Koordinatenursprung und zwei Punkte auf einem Einheitskreis (d.h. ein Kreis mit dem Mittelpunkt $M(0;0)$ im kartesischen Koordinatensystem und dem Radius $r=1$) dargestellt werden.

Teilt man den Kreis in 360 gleiche Teile, wird jedes einzelne Stück als Grad bezeichnet. (Notation: $1^{\circ }$ )

Das Bogenmaß ist eine weitere Möglichkeit zur Messung von Winkeln mit Hilfe des Umfangs des Einheitskreises, dabei gilt:

${\displaystyle {360}^{\circ }\stackrel{\wedge}{=}2\pi .}$

Die Winkeleinheit im Bogenmaß ist “rad” (Radiant), diese wird aber oft weggelassen.

Für die Umrechnung sind folgende Beziehungen wichtig:

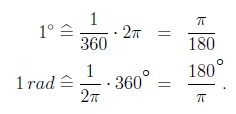
Bei den Berechnungen im Taschenrechner muss man auf richtige Einstellung achten: DEG steht für Grad (Degree) und RAD für Radiant!

11.1.2 Beziehungen am rechtwinkligen Dreieck

In einem rechtwinkligen Dreieck kann das Verhältnis zweier Seiten in Abhängigkeit eines Winkels dargestellt werden. Die längste Seite bezeichnet man Hypotenuse c (den gegenüberliegenden Winkel als $\gamma$), die beiden anderen werden Katheten genannt: Gegenkathete a (gegenüberliegender Winkel ist $\alpha$) und Ankathete b (gegenüberliegender Winkel ist $\beta$).

Es gelten folgende Definitionen:

Sinus:	$\sin \alpha =$	$\frac{\text{Gegenkathete}}{\text{Hypothenuse}}$	$=\frac{a}{c}$
Kosinus:	$\cos \alpha =$	$\frac{\text{Ankathete}}{\text{Hypothenuse}}$	$=\frac{b}{c}$
Tangens:	$\tan \alpha =$	$\frac{\text{Gegenkathete}}{\text{Ankathete}}$	$=\frac{a}{b}$
Kotangens:	$\cot \alpha =$	$\frac{\text{Ankathete}}{\text{Gegenkathete}}$	$=\frac{b}{a}$

Diese Definitionen lassen sich zur Veranschaulichung gut auf den Einheitskreis übertragen:

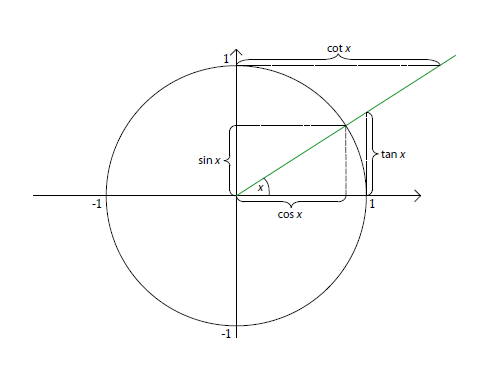
Da die Winkelbeziehungen über den Einheitskreis definiert sind, lässt sich der Satz von Pythagoras anwenden ($a^2+b^2=c^2$) und man erhält einen sehr wichtigen Satz:

${\displaystyle {\sin }^{2}x+{\cos }^{2}x=1.}$

Dieser Satz wird auch als “Trigonometrischer Pythagoras” bezeichnet.

Weiterhin gilt für die Winkelbeziehungen folgende Periodizität, die sich aus der Definition ableiten lässt und auch sehr gut in der grafischen Darstellung der jeweiligen Funktion widerspiegelt. (Diese wird weiter unten behandelt.)

${\displaystyle \begin{array}{rcl}\sin ({180}^{\circ }-\alpha )& =& \sin \alpha \\ \cos ({180}^{\circ }-\alpha )& =& -\cos \alpha \\ & & \\ \sin ({180}^{\circ }+\alpha )& =& -\sin \alpha \\ \cos ({180}^{\circ }+\alpha )& =& -\cos \alpha \\ & & \\ \sin ({360}^{\circ }-\alpha )& =& -\sin \alpha \\ \cos ({360}^{\circ }-\alpha )& =& \cos \alpha \\ & & \end{array}}$

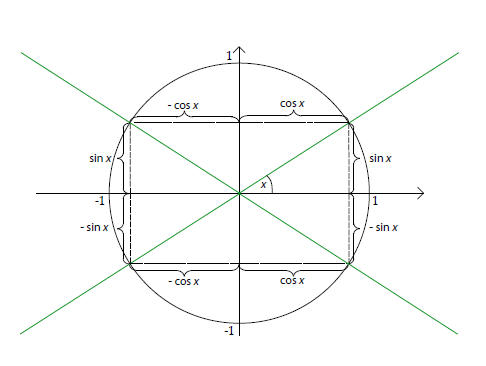
Für die Winkel ${360}^{\circ }+\alpha$ ergibt sich wieder derselbe Winkel, weil das einer Drehung von ${360}^{\circ }$ (oder $2\pi$) im Einheitskreis entspricht.

11.1.3 Grafische Darstellung der Sinus- und Kosinusfunktion

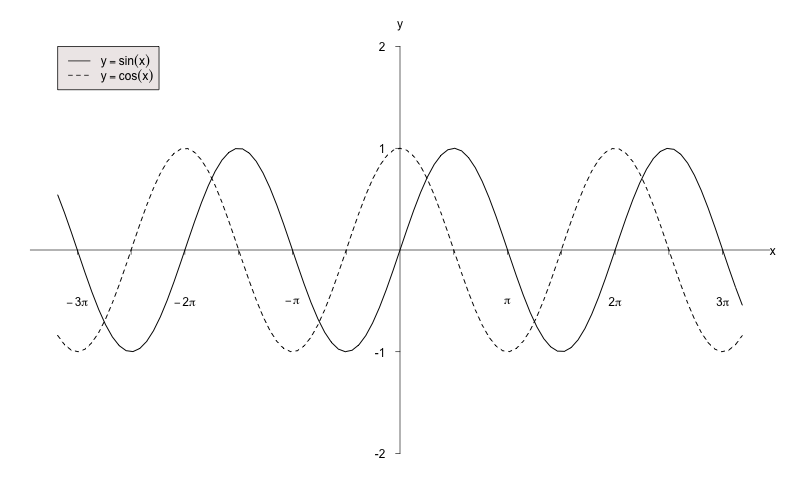
Anhand der Funktionsgraphen lassen sich grundlegende Funktionseigenschaften erkennen:

• Die Sinus- und Kosinusfunktionen sind periodisch. Die kleinste Periode ist $2\pi$, deshalb gilt

  ${\displaystyle \begin{array}{rcl}\sin (x+2\pi )& =& \sin x\\ \cos (x+2\pi )& =& \cos x.\end{array}}$
Hier ist der Winkel x in Bogenmaß zu wählen.

• Die Sinusfunktion ist punktsymmetrisch, denn es gilt

  ${\displaystyle \sin (-x)=-\sin \left(x\right).}$

• Die Kosinusfunktion ist achsensymmetrisch zur $y$-Achse, denn es gilt

  ${\displaystyle \cos (-x)=\cos \left(x\right).}$

• Sinus- und Kosinusfunktion sind wie folgt miteinander verknüpft:

  ${\displaystyle \begin{array}{rcl}\sin (x+\frac{\pi }{2})& =& \cos \left(x\right)\\ \cos (x+\frac{\pi }{2})& =& -\sin \left(x\right).\end{array}}$

11.1.4 Umkehrfunktionen für Sinus- und Kosinusfunktion

Wie bereits bekannt ist, lassen sich nur solche Funktionen umkehren, die streng monoton steigend bzw. streng fallend sind. Ist dies nicht der Fall, muss ein geeigneter Abschnitt der Funktion gewählt werden, auf dem die Funktion streng monoton fallend bzw. steigend ist. Die Umkehrfunktion einer trigonometrischen Funktion heißt Arcusfunktion.

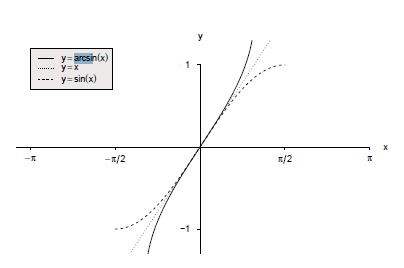
Wenn man den Verlauf der $\sin$-Funktion betrachtet, bietet sich das Intervall $[-\frac{\pi }{2};\frac{\pi }{2}]$ für die Umkehrfunktion an, weil die $\sin$-Funktion in diesem Intervall monoton steigend ist. Die Umkehrfunktion bezeichnet man dann als

${\displaystyle f\left(x\right)=\arcsin \left(x\right)={\sin }^{-1}\left(x\right).}$ Dabei darf der Ausdruck ${\sin }^{-1}\left(x\right)$ nicht mit dem reziproken Wert $\frac{1}{\sin \left(x\right)}$ verwechselt werden.

Der Definitionsbereich ist dann $[-1;1]$ und Wertebereich $[-\frac{\pi }{2};\frac{\pi }{2}]$.

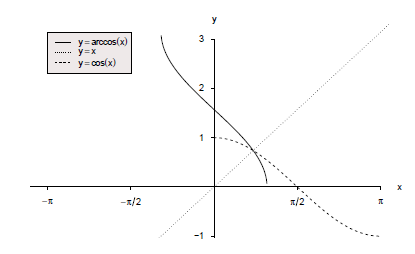
Für die $\cos$-Funktion kann man das Intervall $[0;\pi ]$ wählen, da die Funktion in diesem Abschnitt streng monoton fallend ist. Die Umkehrfunktion wird als

${\displaystyle f\left(x\right)=\arccos \left(x\right)={\cos }^{-1}\left(x\right)}$

bezeichnet, der Definitionsbereich ist $[-1;1]$ und der Wertebereich ist $[0;\pi ]$.

Dabei darf der Ausdruck ${\cos }^{-1}\left(x\right)$ nicht mit dem reziproken Wert $\frac{1}{\cos \left(x\right)}$ verwechselt werden.

11.1.5 Additionstheoreme

Für die trigonometrischen Funktionen gelten folgende Beziehungen, die so genannten Additionstheoreme:

${\displaystyle \begin{array}{rcll}& \sin (x\pm y)& =& \sin x\cdot \cos y\pm \sin y\cdot \cos x\\ & \cos (x\pm y)& =& \cos x\cdot \cos y\mp \sin x\cdot \sin y\\ x=y:& \cos \left(2x\right)& =& {\cos }^{2}x-{\sin }^{2}x\\ x=y:& \sin \left(2x\right)& =& 2\sin x\cdot \cos x\end{array}}$

Die Funktionen sin(2x) und cos(2x) ändern sich doppelt so schnell wie sin x bzw. cos x. Bei sin 2x müssen Sie nicht unbedingt Klammern setzen, sin 2x wäre auch korrekt.

11.1.6 Winkeltabelle

Um bestimmte Werte für $\sin x$ und $\cos x$ leichter ermitteln zu können, erhalten Sie eine Tabelle mit den wichtigsten Winkeln:

11.1.7 Hinweise zur Notation und Benutzung des Taschenrechners

Zur Umkehrfunktion der trigonometrischen Funktionen sollten Sie folgenden Sachverhalt beachten:
Man kann schreiben:

$\text{arccos }x={\text{cos}}^{-1}x$, aber es gilt: ${\left(\text{cos }x\right)}^{-1}=\frac{1}{\text{cos }x}$. Es ist wichtig, dass Sie diesen Unterschied kennen, damit es nicht zu Verwechselungen kommt.
Auch das folgende Zitat aus dem Buch "Mathematik für Ingenieure" von M. Knorrenschild (Hanser Verlag) auf Seite 24 kann in diesem Zusammenhang hilfreich sein:

"Auf den meisten Taschenrechnern müssen Sie für arcsin die Tastenfolge inv ⇒ sin oder die Taste sin^-1 wählen. Kein Problem für Sie, denn Sie wissen ja, dass arcsin die Umkehrfunktion (inverse Funktion) von sin ist, also ist arcsin = sin^-1."

Das folgende Video soll die theoretischen Erläuterungen unterstützen: Winkelbeziehungen

Dieses Video ist Bestandteil des Moodle-Projekts innerhalb der HTW Berlin.

11.2 Beispiele

Beispiel 11.2.1

Eine Anwendung der trigonometrischen Funktionen sind die trigonometrischen Gleichungen. Bei diesen ist es wichtig, dass Sie die Periodizität beachten. Falls der Definitionsbereich von $x$ nicht eingeschränkt ist, muss die Lösung zum Beispiel bei 2𝜋-periodischen Funktionen mit $(+2k\pi )$ erweitert werden.

Gesucht sind alle Lösungen für $x$:

${\displaystyle \sin \left(\frac{x}{3}\right)=\frac{\sqrt{3}}{2}.}$

Als erstes muss man den Wert ermitteln, für den der Sinus $\frac{\sqrt{3}}{2}$ ist. Das geschieht entweder durch Berechnung oder durch einen Blick in die Tabelle für Winkelwerte. Man erhält $\frac{\pi }{3}$. Daraus folgt:

${\displaystyle \frac{x_1}{3}=\frac{\pi }{3}.}$

Nach Umstellen der Gleichung ist leicht ersichtlich, dass

${\displaystyle x_1=\pi .}$

Außerdem hat die Sinusfunktion $\sin =\frac{x}{3}$ den gleichen Funktionswert an der Stelle $\frac{2 \mathrm{\pi }}{3}$ (s.Winkeltabelle), also gilt auch

$\frac{{\mathrm{x}}_2}{3}=\frac{2 \mathrm{\pi }}{3 }$
${\displaystyle x_2=2\pi .}$

Außerdem muss bei den trigonometrischen Gleichungen die Periodizität beachtet werden. Die Lösungen lauten also:

${\mathrm{x}}_1=\mathrm{\pi }\pm 6 \mathrm{k\pi }$

und

${\mathrm{x}}_2=2 \mathrm{\pi }\pm 6 \mathrm{k\pi }$

$k=0,\pm 1,\pm 2,...$

Beispiel 11.2.2

Gesucht sind alle Lösungen für $x$ im Intervall $[0;2\pi ]$:

${\displaystyle 2\sin x+\sin \left(2x\right)=0.}$

Zunächst sollten Sie die Gleichung vereinfachen. Aus dem Abschnitt Additionstheoreme ist bekannt, dass $\sin \left(2x\right)=2\sin x\cdot \cos x$ ist. Daraus folgt

${\displaystyle 2\sin x+2\sin x\cdot \cos x=0.}$

Nun kann $2\sin x$ ausgeklammert werden:

${\displaystyle 2\sin x(1+\cos x)=0.}$

Wenn ein Produkt gleich $0$ ist, dann muss mindestens einer der Faktoren auch $0$ sein.

$2\sin x=0$	oder	$1+\cos x=0$
$\sin x=0$	oder	$\cos x=-1.$

Nun kann man die beiden einfachen trigonometrischen Gleichungen lösen. Aus der Tabelle erhält man

$\sin 0=0$

oder

$\cos \pi =-1$

und

$\sin \pi =0$

Außerdem gilt wegen der Periodizität

${\displaystyle \sin \left(2\pi \right)=0.}$

Also sind die Lösungen

$x_1=0\mathrm{, }$

$x_2=\pi \mathrm{, }$

$x_3=2\pi \mathrm{.}$

Die folgenden Pencasts erläutern ausführlich weitere Beispiele:

11.3 Übungen

Die Lösungen zu den hier gestellten Aufgaben finden Sie im Kapitel "Hinweise und Lösungen zu den Übungen". Zu jeder Übung wird eine Bearbeitungszeit vorgegeben.

Übung 11.3.1

Lösen Sie folgende Gleichung:

$\tan x+\sin x=0\mathrm{, }$

$x\in [0;2\pi ].$

Bearbeitungszeit: 8 Minuten

Übung 11.3.2

Lösen Sie die Gleichung

${\cos }^{2}x-2\sin x+2=0\mathrm{, }$

$x\in [0;2\pi ]$.

Bearbeitungszeit: 10 Minuten

Übung 11.3.3

Vereinfachen Sie den folgenden Ausdruck:

${\displaystyle {\sin }^{4}x+\frac{1}{2}{\sin }^2\left(2x\right)+{\cos }^{4}x.}$ Bearbeitungszeit: 10 Minuten

Übung 11.3.4

Vereinfachen Sie folgenden Ausdruck:

${\displaystyle {\sin }^{4}x-{\cos }^{4}x.}$ Bearbeitungszeit: 10 Minuten


Zum Test

• Startseite
• Einführung
• Inhaltsverzeichnis
  • 1 Umstellen von Gleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 2 Potenzen und Wurzeln
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 4 Polynomdivision
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 5 Mengenlehre
    • Theorie
  • 6 Funktionen
    • Theorie
  • 7 Lineare Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 8 Quadratische Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 11 Trigonometrische Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 12 Funktionen in Polarkoordinaten
    • Theorie
    • Beispiele
    • Übungen
    • Test
• 13 Hinweise und Lösungen zu den Übungen
  • 1 Umstellen von Gleichungen
  • 2 Potenzen und Wurzeln
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
  • 4 Polynomdivision
  • 7 Lineare Funktionen
  • 8 Quadratische Funktionen
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
  • 11 Trigonometrische Funktionen
  • 12 Funktionen in Polarkoordinaten
• 14 Hinweise und Lösungen zu den Tests
  • 1 Umstellen von Gleichungen
  • 2 Potenzen und Wurzeln
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
  • 4 Polynomdivision
  • 7 Lineare Funktionen
  • 8 Quadratische Funktionen
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
  • 11 Trigonometrische Funktionen
  • 12 Funktionen in Polarkoordinaten