8 Quadratische Funktionen

Zum Test

8.1 Theorie

8.1.1 Scheitelpunktform

Eine quadratische Funktion ist eine Polynomfunktion zweiten Grades der Form

${\displaystyle y=a_2\cdot x^2+a_1\cdot x+a_0.}$

Die Scheitelpunktform

${\displaystyle y=a{(x-x_s)}^2+y_s}$

ist eine zweite Darstellungsform, an der der Scheitelpunkt $(x_s;y_s)$ direkt abgelesen werden kann. Anhand dieser Darstellung kann ermittelt werden, wie die Normalparabel $y=x^2$ verschoben und gespiegelt wird, denn der $x_{\mathrm{s}}$-Wert des Scheitelpunktes entspricht dem allgemeinen Paramter $c$ und der $y_{\mathrm{s}}$-Wert dem Parameter $d$. Offenbar ist $a_2$ in der ersten Schreibweise der Streckungs- bzw. Stauchungsparameter der Funktion: $a_2=a$

Die erste Form kann durch quadratische Ergänzung in die Scheitelpunktform umgewandelt werden. Dazu erzeugt man eine binomische Formel der Art $x^2+2ax+a^2$, um diese dann als Quadrat ${(x+a)}^2$ zu notieren. Die quadratische Ergänzung und das Verschieben und Spiegeln durch die Parameter werden an den Einführungsbeispielen genauer erläutert und geübt.

8.1.2 Nullstellen

Eine quadratische Funktion kann die $x$-Achse zweimal, einmal oder gar nicht schneiden, wie die folgende Grafik zeigt.

Um die Nullstellen zu ermitteln, muss die quadratische Funktion Null gesetzt werden,

${\displaystyle a_2\cdot x^2+a_1\cdot x+a_0=0}$

da Nullstellen die Schnittpunkte mit der $x$-Achse sind. Nun muss ermittelt werden, für welche $x$-Werte die Funktion Null wird.

8.1.3 Lösungen einer quadratischen Gleichung

Die Lösungen einer quadratischen Gleichung (Nullstellen einer quadratischen Funktion) werden mit der so genannten Mitternachtsformel (auf diese wird hier nicht eingegangen) oder mit der p-q-Formel berechnet. Letztere erfordert die Normalform der quadratischen Gleichung $x^2+px+q=0$ , wobei $p$ und $q$ Parameter sind. Die Lösung lautet

${\displaystyle x_{1,2}=-\frac{p}{2}\pm \sqrt{{\left(\frac{p}{2}\right)}^2-q}}$

Ist ${\left(\frac{p}{2}\right)}^2-q>0$ , dann existieren zwei reelle Lösungen $x_1$ und $x_2$.

Ist ${\left(\frac{p}{2}\right)}^2-q=0$ , so gibt es eine doppelte reelle Lösung.

Ist ${\left(\frac{p}{2}\right)}^2-q<0$ , dann gibt es keine reelle Lösung.

8.1.4 Schnittpunkt einer Parabel mit einer Geraden

Im Unterschied zu dem Schnittpunkt zweier Geraden kann eine Gerade eine Parabel nicht, nur einmal oder zweimal schneiden, wie folgende Grafik zeigt:

Um die Schnittpunkte zu berechnen, müssen beide Funktionsgleichungen gleichgesetzt werden:

${\displaystyle m\cdot x+n=a_2\cdot x^2+a_1\cdot x+a_0.}$

Im Gegensatz zu dem Schnittpunkt zweier Geraden entsteht eine quadratische Gleichung, die zu der Gleichung $x^2+px+q=0$ umgeformt werden kann. Mit Hilfe der p-q-Formel werden die $x$-Werte ermittelt, die die obere Gleichung erfüllen. Nun müssen die $x$-Werte in eine der beiden Funktionsgleichungen eingesetzt werden, um die zugehörigen $y$-Werte zu berechnen.

8.1.5 Schnittpunkt von Parabeln

Auch der Schnittpunkt zweier Parabeln wird ermittelt, indem beide Parabelgleichungen gleichgesetzt werden. Zwei Parabeln können sich ebenfalls in keinem, einem oder zwei Schnittpunkten schneiden.

Die Gleichung wird anschließend nach $0$ umgestellt, sodass eine lineare (wenn die quadratischen Terme sich aufheben) oder eine quadratische Gleichung entsteht. Um quadratische Gleichungen zu lösen, kann wieder die p-q-Formel angewendet werden.

8.1.6 Quadratische Ungleichungen

Quadratische Ungleichungen sind Ungleichungen mit einer Variablen, die im Gegensatz zu den linearen Ungleichungen auch in quadratischer Form vorkommen, wie z.B.

${\displaystyle x^2-5x\le 2x^2+3x-2.}$

Quadratische Ungleichungen haben nach Umstellung eine der folgenden Formen:

Geometrisch bedeutet dies für Fall (1), dass man eine Parabel $f\left(x\right)=a_2\cdot x^2+a_1\cdot x+a_0$ gegeben hat und prüft, für welche reellen Zahlen $x$ die Parabel über bzw. auf der $x$-Achse liegt. Analog dazu sind auch die anderen Fälle auszuwerten.

Zur genauen Ermittlung der Lösungsmenge werden die Nullstellen der Parabel

${\displaystyle f\left(x\right)=a_2\cdot x^2+a_1\cdot x+a_0}$

bestimmt. Anschließend wird durch Zeichnen bzw. das Einsetzen von Probewerten ermittelt, wie die Funktion verläuft, um z.B. bestimmen zu können, in welchem Bereich die Funktion z.B. positiv oder gleich $0$ ist wie bei der Form (1) gefordert.

Die folgenden Videos sollen die theoretischen Erläuterungen unterstützen:

Quadratische Ungleichungen	Die Ellipsen-Funktion
Dieses Videos sind Bestandteil des Moodle-Projekts innerhalb der HTW-Berlin.

8.2 Beispiele

Beispiel 8.2.1

Zeichnen Sie die folgenden quadratischen Funktionen. Gehen Sie dabei schrittweise vor, indem Sie zunächst die Normalparabel zeichnen und diese anschließend verschieben und strecken bzw. stauchen. Sie sollen keine Wertetabelle benutzen, sondern die elementaren Eigenschaften der Funktionskurve beachten.

Lösung:

1.) Zeichnen Sie zuerst die Normalparabel $y=x^2$. Verschieben Sie diese um $1$ nach rechts. Anhand des Parameters $2$ ist ersichtlich, dass die Parabel in $y$-Richtung gestreckt werden muss. Anschließend wird der Graph um $1$ nach unten verschoben.

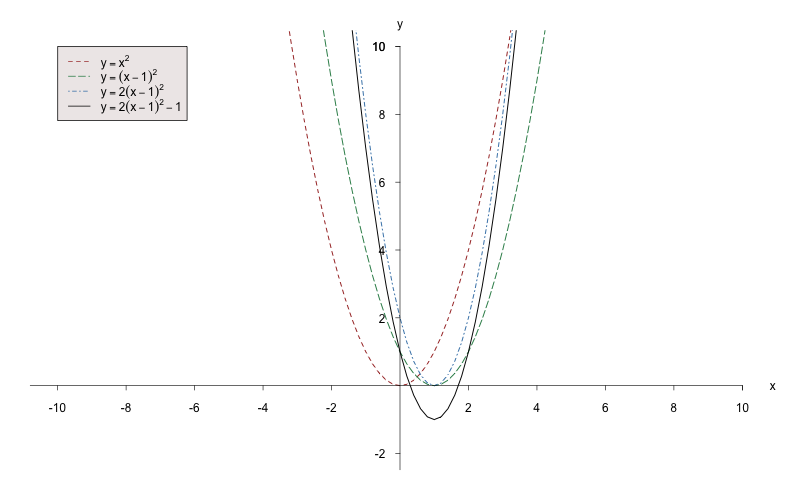
2.) Zeichnen Sie zuerst die Funktion $y=2x^2-2$, indem Sie die Normalparabel in $y$-Richtung strecken und um $2$ nach unten verschieben. Der Betrag von $2x^2-2$ bedeutet geometrisch, dass der Teil der Parabel $2x^2-2$, der negativ ist, an der $x$-Achse gespiegelt wird, denn der Betrag ist definiert durch

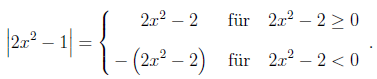
Beispiel 8.2.2

Bringen Sie folgende Funktionsvorschrift durch quadratische Ergänzung in die Scheitelpunktform und zeichnen Sie diese anschließend.

${\displaystyle y=2x^2+12x+24}$

Lösung: Zuerst sollte man $2$ ausklammern:

${\displaystyle y=2(x^2+6x+12).}$

Auf der rechten Seite steht in der Klammer nun fast schon eine binomische Formel, welche jedoch $9$ als Absolutglied haben müsste. Deswegen wird die $12$ als $9+3=3^2+3$ notiert:

${\displaystyle y=2(x^2+2\cdot 3\cdot x+3^2+3).}$

Auf der rechten Seite der Gleichung ergibt sich:

${\displaystyle y=2({(x+3)}^2+3).}$

Die Lösung lautet:

${\displaystyle y=2{(x+3)}^2+6.}$

Es handelt sich um eine Normalparabel, die um $3$ nach links verschoben, in $y$-Richtung gestreckt und um $6$ nach oben verschoben wird.

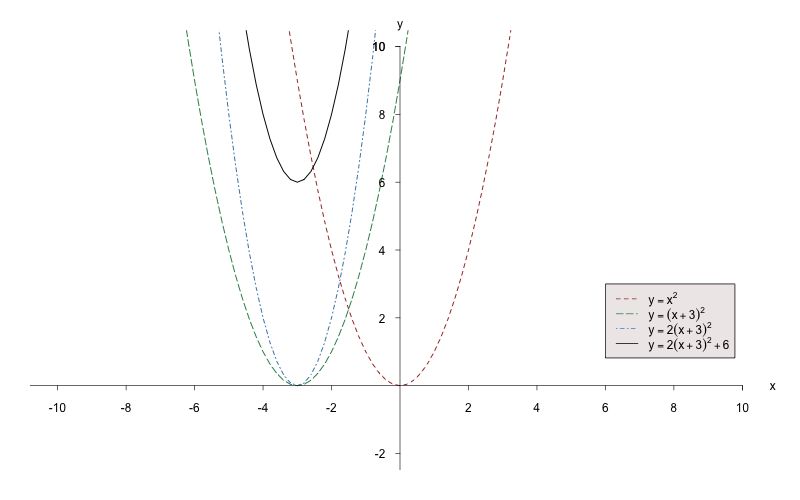
Beispiel 8.2.3

Gegeben sei die Parabel aus Beispiel 8.2.2:

${\displaystyle y=2x^2+12x+24.}$

Lösung:

a) Setzen Sie die Funktion gleich $0$:

${\displaystyle 2x^2+12x+24=0.}$

Stellen Sie die Gleichung nun so um, dass die p-q-Formel angewendet werden kann. Dividieren Sie dafür durch $2$:

${\displaystyle x^2+6x+12=0}$

Wenden Sie nun die p-q-Formel an:

${\displaystyle \begin{array}{rcl}{x}_{1,2}& =& -\frac{6}{2}\pm \sqrt{{\left(\frac{6}{2}\right)}^2-12}\\ & =& -3\pm \sqrt{9-12}\\ & =& -3\pm \sqrt{-3}.\end{array}}$

Da unter der Wurzel eine negative Zahl steht, hat diese Funktion keine reellen Nullstellen. Dieses Ergebnis war bereits an der Zeichnung aus Beispiel 1b zu erkennen.

b) Setzen Sie zunächst beide Funktionsvorschriften gleich:

${\displaystyle 2x^2+12x+24=x^2-10x+47.}$

Nun muss die Gleichung so umgeformt werden, dass die p-q-Formel angewendet werden kann:

${\displaystyle \begin{array}{rcl}2x^2-x^2+12x+10x+24-47& =& 0\\ x^2+22x-23& =& 0.\end{array}}$

Lösen Sie die Gleichung nun mit Hilfe der p-q-Formel:

${\displaystyle \begin{array}{rcl}{x}_{1,2}& =& -\frac{22}{2}\pm \sqrt{{\left(\frac{22}{2}\right)}^2+23}\\ & =& -11\pm \sqrt{121+23}\\ & =& -11\pm \sqrt{144}\\ & =& -11\pm 12\\ x_1=1& & x_2=-23.\end{array}}$

Um die Schnittpunkte zu berechnen, müssen noch die $y$-Werte ermittelt werden:

${\displaystyle \begin{array}{rcl}f\left(1\right)& =& 2\cdot 1^2+12\cdot 1+24=38\\ f(-23)& =& 2\cdot {(-23)}^2+12\cdot (-23)+24=806.\end{array}}$

Die Parabeln schneiden sich in den Punkten

$P_1(1;38)$ und $P_2(-23;806)$.

Beispiel 8.2.4

Lösen Sie folgende quadratische Ungleichung:

${\displaystyle x^2-10x\ge 510-23x.}$

Lösung: Zuerst muss die Ungleichung umgestellt werden:

${\displaystyle \begin{array}{rcl}{x}^2-10x+23x-510& \ge & 0\\ x^2+13x-510& \ge & 0\end{array}}$

Nun können die Nullstellen der Funktion $f\left(x\right)=x^2+13x-510$ berechnet werden. Dafür wird die p-q-Formel angewendet:

${\displaystyle \begin{array}{rcl}{x}_{1,2}& =& -\frac{13}{2}\pm \sqrt{{\left(\frac{13}{2}\right)}^2+510}\\ & =& -6,5\pm \sqrt{42,25+510}\\ & =& -6,5\pm \sqrt{552,25}\\ & =& -6,5\pm 23,5\\ x_1=17& & x_2=-30.\end{array}}$

Es muss überprüft werden, ob die Funktion zwischen den Nullstellen oberhalb oder unterhalb der $x$-Achse verläuft, um zu identifizieren, wo die Funktion Werte größer Null annimmt. Dazu reicht es, einen Wert zwischen $-30$ und $17$ in die Funktion einzusetzen:

${\displaystyle f\left(0\right)=0^2+13\cdot 0-510=-510.}$

Die Funktion verläuft zwischen den Nullstellen unterhalb der $x$-Achse. Also ist die Funktion links von der linken Nullstelle $(-30)$ und rechts von der rechten Nullstelle $\left(17\right)$ größer oder gleich Null:

${\displaystyle \begin{array}{rcl}𝕃& =& (-\infty ,-30]\cup [17,+\infty )\text{ bzw.}\\ 𝕃& =& \{x|\mathrm{(}x\le -\mathrm{30)}\vee \mathrm{(}x\ge \mathrm{17)}\}.\end{array}}$

Bei der Darstellung der Lösungsmenge ist darauf zu achten, dass die Nullstellen eingeschlossen sind, da die Funktion größer oder gleich Null sein soll.

Beispiel 8.2.5

Lösen Sie die folgende Ungleichung durch Zeichnen nach Ermittlung der Nullstellen:

${\displaystyle x(x+7)<5(x+\mathrm{1,6})\mathrm{ .}}$

Lösung: Stellen Sie die Ungleichung zuerst um.

${\displaystyle \begin{array}{rcl}{x}^2+7x& <& 5x+8\\ x^2+7x-5x-8& <& 0\\ x^2+2x-8& <& 0\mathrm{ .}\end{array}}$

Anschließend müssen die Nullstellen ermittelt werden:

${\displaystyle \begin{array}{rcl}{x}_{1,2}& =& -\frac{2}{2}\pm \sqrt{{\left(\frac{2}{2}\right)}^2+8}\\ & =& -1\pm \sqrt{9}\\ & =& -1\pm 3\\ x_1=2& & x_2=-4\mathrm{ .}\end{array}}$

Zur Überprüfung des Funktionsverlaufs soll diese gezeichnet werden. Dazu wird die Funktion in die Scheitelpunktform umgewandelt:

${\displaystyle \begin{array}{rcl}f\left(x\right)& =& x^2+2\cdot 1\cdot x+1^2-9\\ f\left(x\right)& =& {(x+1)}^2-9\mathrm{ .}\end{array}}$

Es handelt sich also um eine Normalparabel, die um $1$ nach links und um $9$ nach unten verschoben wird.

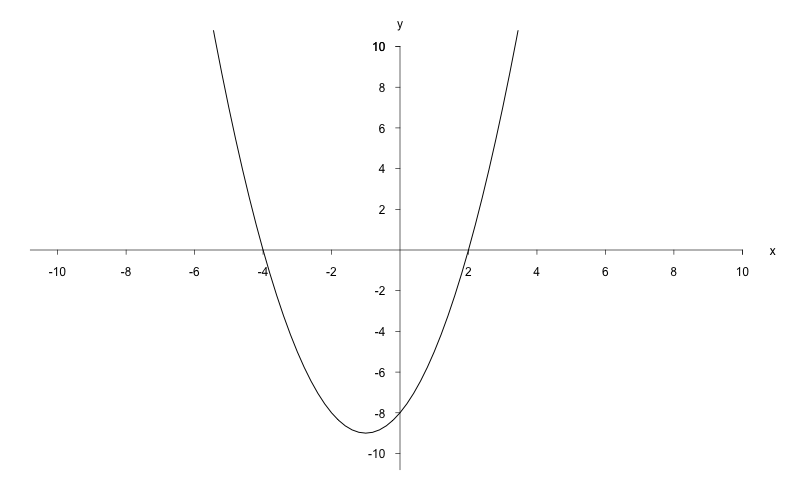
Da diese Parabel nach oben geöffnet ist, nimmt sie zwischen den Nullstellen negative Werte an. Die Lösungsmenge lautet somit

${\displaystyle \begin{array}{rcl}𝕃& =& (-4,2)\text{ bzw.}\\ 𝕃& =& \{x|-4<x<2\}.\end{array}}$

In diesem Fall gehören die Nullstellen nicht zur Lösungsmenge.

Beispiel 8.2.6

Lösen Sie folgenden quadratische Gleichung:

${\displaystyle {\mathrm{x}}^2-\left(1+\frac{1-2 s}{s}\right)\cdot x-\frac{1}{s}=0}$

Lösung: Bevor Sie die p-q-Formel anwenden, sollten Sie den Ausdruck als Bruch schreiben:

${\displaystyle x^2-\left(\frac{s}{s}+\frac{1-2 s}{s}\right)x-\frac{1}{s}=0}$
${\displaystyle x^2-\left(\frac{s+1-2 s}{s}\right)x-\frac{1}{s}=0}$
${\displaystyle x^2-\left(\frac{1- s}{s}\right)x-\frac{1}{s}=0}$

Nun kann die p-q-Formel angewendet werden:

${\displaystyle x_{1,2}=\frac{1-s}{2 s}\pm \sqrt{{\left(\frac{1-s}{2 s}\right)}^2+\frac{1}{s}}}$
${\displaystyle =\frac{1-s}{2 s}\pm \sqrt{\frac{{\left(1-s\right)}^2}{4 s^2}+\frac{1}{s}}}$

Der Ausdruck unter der Wurzel sollte vereinfacht werden. Dafür werden die Brüche gleichnamig gemacht:

${\displaystyle x_{1,2}=\frac{1-s}{2 s}\pm \sqrt{\frac{{\left(1-s\right)}^2}{4 s^2}+\frac{4 s}{4 s^2}}}$
${\displaystyle =\frac{1-s}{2 s}\pm \sqrt{\frac{1-2 s+s^2+4 s}{4 s^2}}}$
${\displaystyle =\frac{1-s}{2 s}\pm \sqrt{\frac{1+2 s+s^2}{4 s^2}}}$
${\displaystyle =\frac{1-s}{2 s}\pm \sqrt{\frac{{\left(1+s\right)}^2}{4 s^2}}}$
${\displaystyle =\frac{1-s}{2 s}\pm \frac{1+s}{2 s}}$

${\displaystyle x_1=\frac{1-s}{2 s}+\frac{1+s}{2 s}}$
${\displaystyle =\frac{1-s+1+s}{2 s}=\frac{2}{2 s}}$
${\displaystyle x_1=\frac{1}{s}}$

${\displaystyle x_2=\frac{1-s}{2 s}-\frac{1+s}{2 s}}$
${\displaystyle =\frac{1-s-1-s}{2 s}=-\frac{2 s}{2 s}}$
${\displaystyle x_2=-1}$

Nun sollten Sie noch eine Probe durchführen:

${\displaystyle x_1=\frac{1}{s}}$
${\displaystyle {\left(\frac{1}{s}\right)}^2-\left(1+\frac{1-2 s}{s}\right)\cdot \frac{1}{s}-\frac{1}{s}=0}$
${\displaystyle \frac{1}{s^2}-\left(\frac{1- s}{s}\right)\cdot \frac{1}{s}-\frac{1}{s}=0}$
${\displaystyle \frac{1}{s^2}-\frac{1- s}{s^2}-\frac{1}{s}=0}$
${\displaystyle \frac{1}{s^2}-\frac{1- s}{s^2}-\frac{s}{s^2}=0}$
${\displaystyle \frac{1-1+ s-s}{s^2}=0}$
${\displaystyle 0=0}$


${\displaystyle x_2=-1}$
${\displaystyle {\left(-1\right)}^2-\left(1+\frac{1-2 s}{s}\right)\cdot \left(-1\right)-\frac{1}{s}=0}$
${\displaystyle 1+\frac{1-s}{s}-\frac{1}{s}=0}$
${\displaystyle \frac{s}{s}+\frac{1-s}{s}-\frac{1}{s}=0}$
${\displaystyle \frac{s+1-s-1}{s}=0}$
${\displaystyle 0=0}$

Somit ist die Lösung:

${\displaystyle 𝕃=\left\{\left(\frac{\mathit{1}}{s}\right);-1\right\}}$

Die folgenden Pencasts erläutern ausführlich fünf weitere Beispiele:

8.3 Übungen

Die Lösungen zu den hier gestellten Aufgaben finden Sie im Kapitel "Hinweise und Lösungen zu den Übungen". Zu jeder Übung wird eine Bearbeitungszeit vorgegeben.

Übung 8.3.1

Zeichnen Sie die folgenden Parabeln, indem Sie schrittweise die Normalparabel verschieben, stauchen oder strecken.

a)	$y=-{(x-1)}^2+1$
b)	$y=|-{(x+1)}^2|+2$
c)	$y=x^2+14x+52$
d)	$y=5x^2-30x+2$.

Bearbeitungszeit: a) 3 Minuten, b) 5 Minuten, c) 7 Minuten, d) 8 Minuten

Übung 8.3.2

Berechnen Sie die Nullstellen folgender quadratischer Funktionen.

Bearbeitungszeit: a) 5 Minuten, b) 2 Minuten, c) 10 Minuten d) 10 Minuten

Übung 8.3.3

Gegeben sei die Parabel

${\displaystyle y=4x^2+10x-3.}$

Berechnen Sie die Schnittpunkte mit

Bearbeitungszeit: a) 4 Minuten, b) 6 Minuten, c) 8 Minuten

Übung 8.3.4

Berechnen Sie die Lösungsmenge folgender quadratischer Ungleichungen

a)	$x^2+3x-2<-2x^2-3x+7$
	indem Sie die Funktion nach der Nullstellenermittlung zeichnen.
b)	$x\cdot \left(\frac{x+2}{5}\right)-\frac{x+3}{15}>\frac{x+5}{3}$
	durch Einsetzen eines Probewertes nach Ermittlung der Nullstellen.
c)	$(2x+8)(2x-8)<4x$
	durch ein selbstgewähltes Verfahren.

Bearbeitungszeit: a) 8 Minuten, b) 10 Minuten, c) 10 Minuten

Zum Test

• Startseite
• Einführung
• Inhaltsverzeichnis
  • 1 Umstellen von Gleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 2 Potenzen und Wurzeln
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 4 Polynomdivision
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 5 Mengenlehre
    • Theorie
  • 6 Funktionen
    • Theorie
  • 7 Lineare Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 8 Quadratische Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 11 Trigonometrische Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 12 Funktionen in Polarkoordinaten
    • Theorie
    • Beispiele
    • Übungen
    • Test
• 13 Hinweise und Lösungen zu den Übungen
  • 1 Umstellen von Gleichungen
  • 2 Potenzen und Wurzeln
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
  • 4 Polynomdivision
  • 7 Lineare Funktionen
  • 8 Quadratische Funktionen
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
  • 11 Trigonometrische Funktionen
  • 12 Funktionen in Polarkoordinaten
• 14 Hinweise und Lösungen zu den Tests
  • 1 Umstellen von Gleichungen
  • 2 Potenzen und Wurzeln
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
  • 4 Polynomdivision
  • 7 Lineare Funktionen
  • 8 Quadratische Funktionen
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
  • 11 Trigonometrische Funktionen
  • 12 Funktionen in Polarkoordinaten