2 Potenzen und Wurzeln

Zum Test

2.1 Theorie

Im folgenden Abschnitt sollen komplizierte Gleichungen, die Potenzen und Wurzeln enthalten, vereinfacht werden. Als Grundlage dienen die Potenz- und Wurzelgesetze:

Multiplikation bzw. Division von Potenzen mit gleicher Basis:
$\begin{array}{rcl} a^{n} \cdot a^{m} & = & a^{(n + m)} \\ a^{n} : a^{m} & = & a^{(n - m)} \end{array}$
Multiplikation bzw. Division von Potenzen mit gleichem Exponenten:
$\begin{array}{rcl} a^{n} \cdot b^{n} & = & {(a \cdot b)}^{n} \\ a^{n} : b^{n} & = & {(a : b)}^{n} \end{array}$
Potenzieren von Potenzen:
${(a^{n})}^{m} = a^{(n \cdot m)}$

Zudem gelten folgende Definitionen:

$a^{- n}$	=	$\frac{1}{a^{n}}$	für $a \neq 0$

$a^{0}$	=	$1$	für $a \neq 0$

$\sqrt[m]{a^{n}}$	=	$a^{n / m}$	für $a \geq 0$ und $n, m$ positiv ganzzahlig

Im gesamten Material setzen wir voraus, dass Ausdrücke in einem Nenner jeweils verschieden von Null sind, die Division durch 0 wird nicht gesondert ausgeschlossen.

2.2 Beispiele

Beispiel 2.2.1

Vereinfachen Sie folgenden Term

(a \neq 0)

unter Anwendung der jeweiligen Gesetze so weit wie möglich:

\frac{5 a^{n} b^{n + 4} c^{2 n + 1}}{a b x^{n + 1} y^{n + 2} z^{n + 3}} : \frac{3 a^{n - 1} b^{3} c^{n + 1}}{2 x y^{2 - n} z^{3 - n}}

Ein möglicher erster Schritt ist das Ausführen der Division:

\frac{5 a^{n} b^{n + 4} c^{2 n + 1} \cdot 2 x y^{2 - n} z^{3 - n}}{a b x^{n + 1} y^{n + 2} z^{n + 3} \cdot 3 a^{n - 1} b^{3} c^{n + 1}}

Es ist wieder ratsam, den Term zu sortieren, um die Übersichtlichkeit zu erhöhen:

\frac{10 a^{n} b^{n + 4} c^{2 n + 1} x y^{2 - n} z^{3 - n}}{3 a a^{n - 1} b b^{3} c^{n + 1} x^{n + 1} y^{n + 2} z^{n + 3}}

Entweder kürzt man nun direkt oder schreibt einen Term für jede Basis, um die Gesetze leichter anwenden zu können:

\begin{array}{rcl} \frac{10}{3} \cdot \frac{a^{n}}{a \cdot a^{n - 1}} \cdot \frac{b^{n + 4}}{b \cdot b^{3}} \cdot \frac{c^{2 n + 1}}{c^{n + 1}} \cdot \frac{x}{x^{n + 1}} \cdot \frac{y^{2 - n}}{y^{n + 2}} \cdot \frac{z^{3 - n}}{z^{n + 3}} \end{array}

Nun kann das Gesetz für die Division von Potenzen mit gleicher Basis angewendet werden:

\begin{array}{rcl} \frac{10}{3} \cdot a^{n - (1 + n - 1)} \cdot b^{n + 4 - (1 + 3)} \cdot c^{2 n + 1 - (n + 1)} \cdot x^{1 - (n + 1)} \cdot y^{2 - n - (n + 2)} \cdot z^{3 - n - (n + 3)} \\ = & \frac{10}{3} \cdot a^{n - 1 - n + 1} \cdot b^{n + 4 - 1 - 3} \cdot c^{2 n + 1 - n - 1} \cdot x^{1 - n - 1} \cdot y^{2 - n - n - 2} \cdot z^{3 - n - n - 3} \\ = & \frac{10}{3} \cdot a^{0} \cdot b^{n} \cdot c^{n} \cdot x^{- n} \cdot y^{- 2 n} \cdot z^{- 2 n} \\ = & \frac{10}{3} \cdot \frac{{1⋅b}^{n} c^{n}}{x^{n} y^{2 n} z^{2 n}} \\ = & \frac{10}{3} \cdot {(\frac{b c}{x y^{2} z^{2}})}^{n} \end{array}

Beispiel 2.2.2

Der folgende Term ist so weit wie möglich durch Anwendung der Potenz- und Wurzelgesetze zu vereinfachen:

\frac{125 a^{7} b^{11}}{138 x^{10} y^{8}} : \frac{175 a^{4} b^{18}}{92 x^{9} y^{8}}

Lösung: Zuerst wird die Division durchgeführt, um die Terme auf einen Bruch zu bringen:

= \frac{125 a^{7} b^{11} \cdot 92 x^{9} y^{8}}{138 x^{10} y^{8} \cdot 175 a^{4} b^{18}}

Falls es schwer fällt richtig zu kürzen, sollte man Zähler und Nenner sortieren:

= \frac{125 \cdot 92 a^{7} b^{11} x^{9} y^{8}}{138 \cdot 175 a^{4} b^{18} x^{10} y^{8}}

Treten in derartigen Ausdrücken ganzzahlige Faktoren auf, können Sie diese leicht durch Zerlegung in Primfaktoren (Primzahlen: natürliche Zahlen, die nur durch $1$ oder durch sich selbst teilbar sind) in Potenzausdrücke umschreiben.

Dabei werden beginnend mit $2$ die ganzzahligen Teiler der gegebenen Zahl in wachsender Reihenfolge ermittelt. Oft sind diese Faktoren mehrfach vorhanden, wodurch entsprechenden Potenzen auftreten:

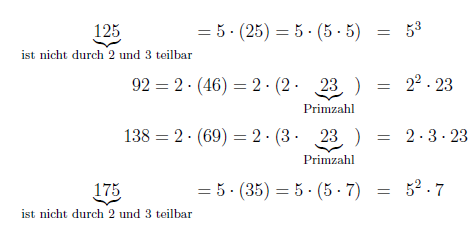
Durch Anwendung von Potenzgesetzen können Sie nun weiter vereinfachen:

\frac{125 \cdot 92}{138 \cdot 175} = \frac{(5^{3}) \cdot (2^{2} \cdot 23)}{(2 \cdot 3 \cdot 23) \cdot (5^{2} \cdot 7)} = \frac{5^{3 - 2} \cdot 2^{2 - 1} \cdot 23^{1 - 1}}{3 \cdot 7} = \frac{5 \cdot 2}{3 \cdot 7} = \frac{10}{21}

Tipp: Manchmal hilft es die Terme einzeln zu betrachten, damit direkt erkannt wird, welches Gesetz angewendet werden kann:

\begin{array}{rcl} = & \frac{10}{21} \cdot \frac{a^{7}}{a^{4}} \cdot \frac{b^{11}}{b^{18}} \cdot \frac{x^{9}}{x^{10}} \cdot \frac{y^{8}}{y^{8}} \\ = & \frac{10}{21} \cdot a^{7 - 4} \cdot b^{11 - 18} \cdot x^{9 - 10} \\ = & \frac{10}{21} \cdot a^{3} \cdot b^{- 7} \cdot x^{- 1} \\ = & \frac{10}{21} \cdot \frac{a^{3}}{b^{7} x} \end{array}

Der folgende Pencast erläutert ausführlich eine weitere Beispielaufgabe:

2.3 Übungen

Die Lösungen zu den hier gestellten Aufgaben finden Sie im Kapitel "Hinweise und Lösungen zu den Übungen". Zu jeder Übung wird eine Bearbeitungszeit vorgegeben.

Übung 2.3.1

Vereinfachen Sie so weit wie möglich:

{(\frac{a^{- 4} b^{- 5}}{x^{- 1} y^{3}})}^{2} \cdot {(\frac{a^{- 2} x}{b^{3} y^{2}})}^{- 3}

Bearbeitungszeit: 8 Minuten

Übung 2.3.2

Vereinfachen Sie bitte folgenden Ausdruck: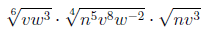

Bearbeitungszeit: 8 Minuten

Übung 2.3.3

Vereinfachen Sie bitte folgenden Ausdruck: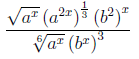

Bearbeitungszeit: 10 Minuten

Zum Test

letztes Kapitel: Umstellen von Gleichungen

nächstes Kapitel: Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz

Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz

Impressum | Datenschutzerklärung