9 Potenz- und Wurzelfunktionen, Wurzelgleichungen

Zum Test

9.1 Theorie

9.1.1 Potenzfunktionen

Eine Funktion der Form

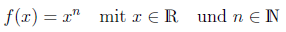
heißt eine Potenzfunktion vom Grade $n$ . Der Definitionsbereich ist der Bereich der reellen Zahlen. Der Funktionsgraph stellt die Parabel $n$ -ter Ordnung dar.

Eigenschaften der Potenzfunktion $f (x) = x^{n}$ :

$n$ ist eine gerade Zahl ( $n = 2 k, k \in ℕ$ )
- Der Graph der Funktion ist achsensymmetrisch zur $y$ -Achse, d.h. Funktion ist gerade. Für alle $x \in ℝ$ gilt:
  $f (x) = f (- x)$
- $(0; 0)$ , $(-1; 1)$ und $(1; 1)$ gehören zu dem Graphen.
- Die Funktion ist für $x \in (- \infty; 0)$ streng monoton fallend und für $x \in (0; \infty)$ streng monoton wachsend.
- Der Wertebereich der Funktion ist $W_{f} \in [0; \infty)$
- Beispiele:
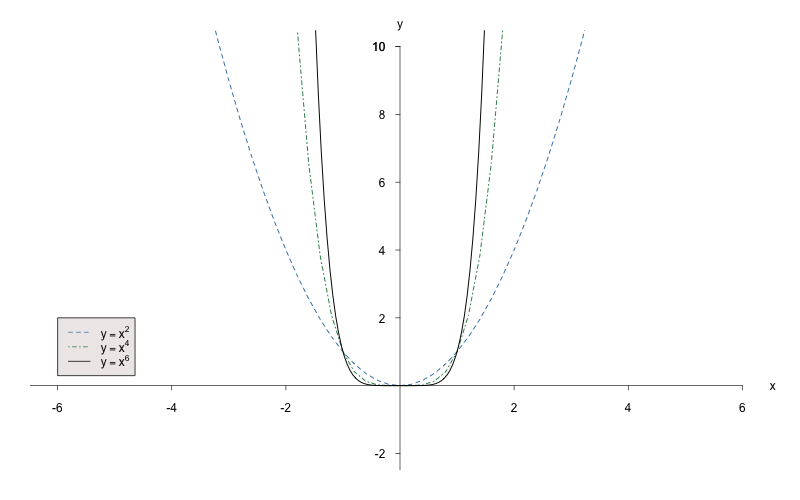
$n$ ist eine ungerade Zahl ( $n = 2 k + 1, k \in ℕ$ )
- Der Graph der Funktion ist punktsymmetrisch zum Koordinatenursprung, d.h. Funktion ist ungerade. Für alle $x \in ℝ$ gilt:
  $f (x) = - f (- x) .$
- $(0; 0)$ , $(- 1; - 1)$ und $(1; 1)$ gehören zu dem Graphen.
- Die Funktion ist für $x \in ℝ$ streng monoton steigend.
- Der Wertebereich ist $W_{f} \in (- \infty; \infty)$
- Beispiele:

Für $n = 0$ , $n = 1$ und $n = 2$ ergeben sich die bereits bekannten Potenzfunktionen

$f (x) = x^{0} = 1$ (konstante Funktion)

$f (x) = x^{1} = x$ (lineare Funktion)

$f (x) = x^{2}$ (quadratische Funktion)

Die Potenzfunktion der Form

f (x) = x^{- n}

mit

x \in ℝ, (x \neq 0)

und

n \in ℕ

nennt man Hyperbelfunktion vom Grade $n$ , der Graph ist eine Hyperbel $n$ -ter Ordnung. Der Definitionsbereich umfasst alle reellen Zahlen außer $0$ .

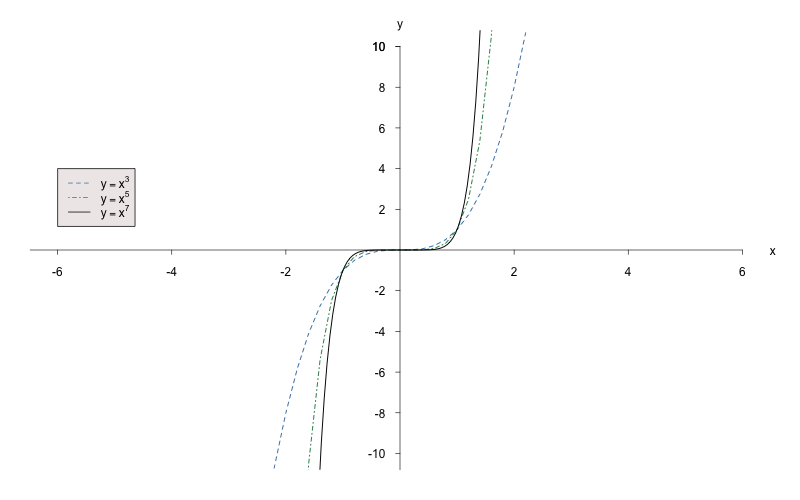
Eigenschaften der Hyperbelfunktion $f (x) = x^{- n}$ :

$n$ ist eine gerade Zahl ( $n = 2 k, k \in ℕ$ )
- Der Graph der Funktion ist achsensymmetrisch zur $y$ -Achse, d.h. Funktion ist gerade. Für alle $x \in ℝ$ gilt:
  $f (x) = f (- x) .$
- Der Graph besteht aus 2 Hyperbel-Ästen und schmiegt sich an die positive $y$ -Achse und an die $x$ -Achse.
- $(- 1; 1)$ und $(1; 1)$ gehören zu dem Graphen.
- Die Funktion ist für $x \in (- \infty; 0)$ streng monoton wachsend und für $x \in (0; \infty)$ streng monoton fallend (zwei monotone Hyperbel-Äste).
- Der Wertebereich ist $W_{f} \in ℝ^{+}$
- Beispiele:
$n$ ist eine ungerade Zahl ( $n = 2 k + 1, k \in ℕ$ )
- Der Graph der Funktion ist punktsymmetrisch zum Koordinatenursprung, d.h. Funktion ist ungerade. Für alle $x \in ℝ$ gilt:
  $f (x) = - f (- x) .$
- Der Graph besteht aus zwei Hyperbel-Ästen, die sich jeweils an die positiven und negativen Achsen anschmiegen.
- $(- 1; - 1)$ und $(1; 1)$ gehören zu dem Graphen.
- Die Funktion ist sowohl $x \in (- \infty; 0)$ als auch für für $x \in (0; \infty)$ streng monoton fallend (zwei monotone Hyperbel-Äste).
- Der Wertebereich ist $W_{f} \in ℝ_{0} = ℝ \ \{0\}$ .
- Beispiele:

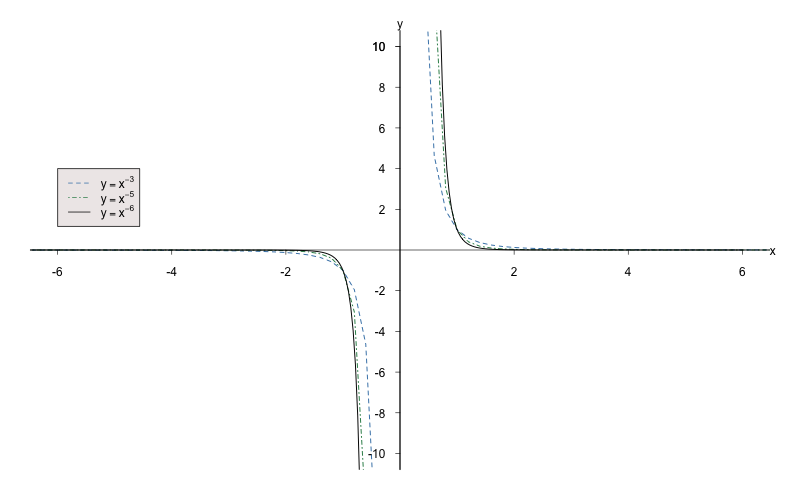
9.1.2 Wurzelfunktionen

Die Umkehrfunktion der Potenzfunktion ist die Wurzelfunktion

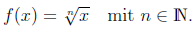
Der Definitionsbereich ist

für gerade $n$ :	$D_{f} \in [0; \infty)$ bzw.
für ungerade $n$ :	$D_{f} \in ℝ$ .

Wie schon aus dem Abschnitt über die Umkehrfunktion bekannt ist, spielt für die Umkehrbarkeit einer Funktion die Monotonie eine wichtige Rolle. Ein Hindernis der Umkehrbarkeit der Potenzfunktion ist der Monotoniewechsel bei den geraden Potenzfunktionen. Also muss man den Definitionsbereich geeignet einschränken, damit man eine Umkehrfunktion bilden kann. Bei den ungeraden Potenzfunktionen treten solche Probleme nicht auf, weil diese Funktionen auf gesamten Definitionsbereich monoton steigend sind.

Eine Wurzelfunktion ist eine Potenzfunktion mit einem rationalem Exponenten, denn es gilt

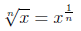
9.1.3 Wurzelgleichungen

Gleichungen, bei denen im Radikanden einer Wurzel eine Variable auftritt, nennt man Wurzelgleichungen. Der Umgang mit Wurzelgleichungen wird am besten an den nachfolgenden Beispielen deutlich, in denen die Lösung solcher Gleichungen ausführlich erklärt wird. Zu beachten ist, dass Wurzelausdrücke im Bereich der reellen Zahlen nur für nicht-negative Radikanden erklärt sind. Deshalb muss man immer den entsprechenden Definitionsbereich vor der Bestimmung der Lösungsmenge untersuchen.

9.2 Beispiele

Beispiel 9.2.1

Gesucht ist die Umkehrfunktion für die Funktion

f (x) = x^{2} - 1, x \geq 0

Bestimmen Sie anschließend den Definitionsbereich der Umkehrfunktion!

Lösung: Zuerst muss die Funktionsgleichung nach $x$ umgestellt werden:

\begin{array}{rcl} y & = & x^{2} - 1 \\ y + 1 & = & x^{2} \\ \pm \sqrt{y + 1} & = & x \end{array}

Gesucht ist nur $+ \sqrt{y + 1}$ wegen $x \geq 0$ . Anschließend werden formal die Variablen vertauscht:

y = \sqrt{x + 1}

Somit ist die Umkehrfunktion

f^{- 1} (x) = \sqrt{x + 1}

Nun muss noch der Definitionsbereich ermittelt werden. Für $\sqrt{x + 1}$ muss $x + 1 \geq 0$ gelten, weil der Radikand $x + 1$ nicht negativ sein darf (damit der Wert der Wurzel reell bleibt).

\begin{array}{rcl} x + 1 & \geq & 0 \\ x & \geq & - 1 \end{array}

Der Definitionsbereich ist somit

D_{f} = [- 1; \infty) .

Beispiel 9.2.2

Lösen Sie die Gleichung

\sqrt{x + 5} - 4 = 1 .

Lösung: Zuerst muss der Definitionsbereich bestimmt werden:

\begin{array}{rcl} x + 5 & \geq & 0 \\ x & \geq & - 5 \end{array}

Daraus folgt

x \in [- 5; \infty) .

Jetzt können wir die Gleichung lösen. Durch Quadrieren kann die Wurzel verschwinden. In diesem Beispiel ist es aber nicht sehr sinnvoll, die Gleichung in der ursprünglichen Form zu quadrieren, weil sonst auf der linken Gleichungsseite die 2. binomische Formel entsteht. Also muss die Gleichung umgeformt werden:

\begin{array}{rcl} \sqrt{x + 5} - 4 & = & 1 \\ \sqrt{x + 5} & = & 5 . \end{array}

Nun kann die Gleichung leicht quadriert werden:

{(\sqrt{x + 5})}^{2} = 5^{2} .

Bei diesem Schritt handelt es sich nicht um eine äquivalente Umformung, hier könnten "Scheinlösungen" entstehen.
Durch Anwendung der Potenzgesetze ( ${(\sqrt{a})}^{2} = a$ ) erhält man

\begin{array}{rcl} x + 5 & = & 25 \\ x & = & 20 \end{array}

Nun erfolgt eine Überprüfung, ob das Ergebnis auch Teil des Definitionsbereiches der Funktion ist. Dies trifft für dieses Beispiel zu:

20 \in [- 5; \infty)

Zuletzt setzen wir den gefundenen Wert zur Probe in die Ausgangsgleichung ein:

\begin{array}{rcl} \sqrt{20 + 5} - 4 & = & 1 \\ \sqrt{25} - 4 & = & 1 \\ 5 - 4 & = & 1 \\ 1 & = & 1 \\ wahre Aussage . \end{array}

Die Lösungsmenge lautet somit

L = {20} .

Hinweis: Die gefundenen Lösungen müssen immer kontrolliert werden, da Quadrieren (und Potenzieren mit einem geraden Exponenten allgemein) keine Äquivalenzumformung ist! (d.h. wenn aus der Gleichheit $a = b$ die Gleichheit $a^{2} = b^{2}$ folgt, gilt dies nicht in umgekehrter Richtung!) „Scheinlösungen“ werden durch die Probe (einsetzen in die Ausgangsgleichung) aussortiert.

Beispiel 9.2.3

Gesucht ist die Lösungsmenge der Gleichung

\sqrt{7 x + 8} = 4 + \sqrt{7 x - 24} .

Lösung: Zunächst erfolgt die Bestimmung des Definitionsbereiches. Dabei muss gelten

7 x + 8 \geq 0

und

7 x - 24 \geq 0 .

Löst man beide Ungleichungen nach $x$ auf, so erhält man

x \geq - \frac{8}{7}

und

x \geq \frac{24}{7} .

Daraus folgt für den Definitionsbereich

D = {x | x \geq \frac{24}{7}} .

Nun wird die in der Übung gegebene Gleichung gelöst. In diesem Beispiel können wir keine weitere Vereinfachungen vornehmen, also quadrieren wir auf beiden Seiten (Vorsicht: Auf der rechten Seite entsteht die 1. binomische Formel).

\begin{array}{rcl} {(\sqrt{7 x + 8})}^{2} & = & {(4 + \sqrt{7 x - 24})}^{2} \\ 7 x + 8 & = & 16 + 8 \sqrt{7 x - 24} + (7 x - 24) \\ 16 & = & 8 \sqrt{7 x - 24} \end{array}

Nun wird die Gleichung noch einmal quadriert, um die Wurzel zu beseitigen:

\begin{array}{rcl} 16^{2} & = & {(8 \sqrt{7 x - 24})}^{2} \\ 256 & = & 64 (7 x - 24) \\ 4 & = & 7 x - 24 \\ 28 & = & 7 x \\ x & = & 4 \end{array}

Schließlich wird noch eine Probe durchgeführt:

\begin{array}{rcl} \sqrt{7 \cdot 4 + 8} & = & 4 + \sqrt{7 \cdot 4 - 24} \\ 6 & = & 4 + 2 \\ 6 & = & 6 \\ wahre Aussage . \end{array}

Die Lösungsmenge lautet somit

L = {4} .

Der folgende Pencast erläutert ausführlich eine weitere Beispielaufgabe:

9.3 Übungsaufgaben

Die Lösungen zu den hier gestellten Aufgaben finden Sie im Kapitel "Hinweise und Lösungen zu den Übungen". Zu jeder Übung wird eine Bearbeitungszeit vorgegeben.