4 Polynomdivision

Zum Test

4.1 Theorie

Polynome sind Ausdrücke der Form

P_{n} (x) = \sum_{i = 0}^{n} a_{i} x^{i} = a_{n} x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{1} x + a_{0}

$a_{i} \in ℝ; i, n \in ℕ_{0} .$

Dabei werden die $a_{i}$ als Koeffizienten bezeichnet und es wird $a_{n} \neq 0$ vorausgesetzt; $n$ ist der Grad des Polynoms (Polynom $n$ -ten Grades).

Ein Polynom $n$ -ten Grades kann durch ein anderes Polynom $m$ -ten Grades dividiert werden, wenn $n \geq m$ erfüllt ist:

\frac{P_{n} (x)}{P_{m} (x)} = P_{n} (x) : P_{m} (x) = \dots

Das Verfahren funktioniert analog zur schriftlichen Division von Zahlen mit Rest. Dabei wird vom Dividenden das passende Vielfache des Divisors abgezogen, bis die Rechnung komplett aufgeht oder ein Rest übrig bleibt, der nicht mehr durch den Divisor teilbar ist. Eine genaue Erläuterung der Vorgehensweise erfolgt in den Beispielen.

Die Polynomdivision ist u.a. hilfreich bei der Ermittlung von Nullstellen von Polynomen. Es ist i.d.R. kompliziert bzw. unmöglich, die Nullstellen eines Polynoms höheren als zweiten Grades exakt zu berechnen. Wenn man allerdings eine Nullstelle $x_{*}$ gefunden hat, kann das Polynom $P_{n} (x)$ ohne Rest durch das Binom $x - x_{*}$ geteilt werden:

\frac{P_{n} (x)}{x - x_{*}} = P_{n} (x) : (x - x_{*}) = P_{n - 1} (x)

Das enstehende Restpolynom $P_{n - 1} (x)$ wird dann weiter untersucht. Ist zum Beispiel zunächst ein Polynom 3. Grades gegeben,

\frac{P_{3} (x)}{x - x_{*}} = P_{3} (x) : (x - x_{*}) = P_{2} (x)

kann dann für das Restpolynom $P_{2} (x)$ die $p$ - $q$ -Formel zur exakten Berechnung der weiteren zwei Nullstellen eingesetzt werden.

4.2 Beispiele

Beispiel 4.2.1

Gesucht ist das Resultat der Division

(x^{2} + 2 x^{3} - 1) : (- 2 + x^{2})

Lösung: Bevor mit der Division begonnen werden kann, müssen die Terme absteigend nach dem Grad des Polynoms zu

(2 x^{3} + x^{2} - 1) : (x^{2} - 2)

sortiert werden, da man zuerst die größte Potenz dividiert. Nun überlegt man, wie oft $(x^{2} - 2)$ in $2 x^{3}$ enthalten ist. Dafür geht man wie folgt vor: Zuerst teilt man $2 x^{3} : x^{2} = 2 x$ , um das erste Glied des Ergebnisses zu berechnen.

Nun multipliziert man das erste Teilergebnis mit dem Divisor und subtrahiert das Ergebnis vom Dividenden, um zu ermitteln, welcher Rest noch dividiert werden muss. $2 x \cdot (x^{2} - 2) = 2 x^{3} - 4 x$

Man verwendet folgende Notation, die analog zur schriftlichen Division funktioniert. Zur besseren Übersicht sollten gleiche Potenzen untereinander geschrieben werden:

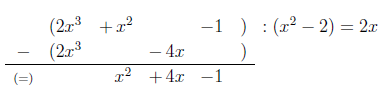
Die -1 entsteht als Übertrag aus der ersten Zeile.

Der Rest ist also $x^{2} + 4 x - 1$ und hat bereits nur noch einen Polynomgrad von 2. Nun dividiert man wieder $x^{2} : x^{2} = 1$ und multipliziert das Ergebnis mit $(x^{2} - 2)$ . Anschließend kann die Berechnung fortgeschrieben werden:

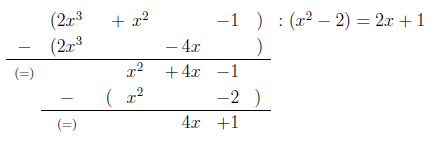
Nun entsteht ein Rest $4 x + 1$ , der jedoch nicht ganzzahlig durch $x^{2} - 2$ teilbar ist, da das Restpolynom einen kleineren Grad als der Divisor hat. Deswegen lautet das Ergebnis:

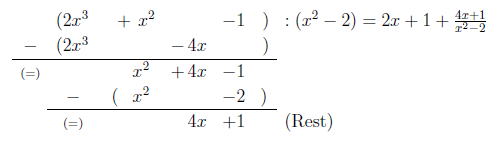
Dies kann auch wie folgt geschrieben werden:

\frac{2 x^{8} + x^{2} - 1}{x^{2} - 1} = 2 x + 1 + \frac{4 x + 1}{x^{2} - 1} bzw . 2 x^{8} + x^{2} - 1 = (x^{2} - 1) (2 x + 1) + 4 x + 1

Beispiel 4.2.2

Das folgende Beispiel zeigt, dass auch eine Polynomdivision mit zwei Variablen funktioniert. Es soll folgende Division ausgeführt werden:

(a^{3} - b^{3}) : (a - b)

Lösung: Hier sind die Terme nach Variablen und Potenz bereits sortiert und es kann $(a^{3} - b^{3})$ durch $(a - b)$ geteilt werden. Offenbar gelten:

\begin{array}{rcl} a^{3} : a & = & a^{2} \\ a^{2} \cdot (a - b) & = & a^{3} - a^{2} b \end{array}

Nun kann der erste Schritt ausgeführt werden:

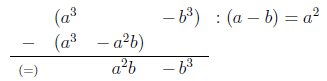
Der entstandene Rest ist $(a^{2} b + b^{3})$ , der nun durch $(a - b)$ dividiert werden muss:

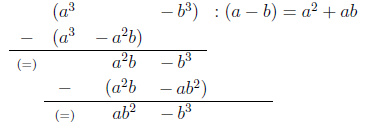
Der neue Rest ist $(a \cdot b^{2} + b^{3})$ . Die Schritte werden so lange fortgeführt, bis die Rechnung aufgegangen ist oder ein nicht teilbarer Rest übrig bleibt:

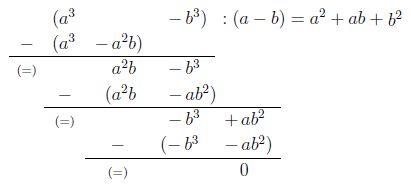
Polynomdivision

Das Resultat ist eine binomische Formel:

\frac{a^{3} - b^{3}}{a - b} = a^{2} + ab + b^{2} bzw . a^{3} - b^{3} = (a - b) (a^{2} + ab + b^{2})

In diesem Fall geht die Division ohne Rest auf und die Übung ist damit gelöst.

4.3 Übungen

Die Lösungen zu den hier gestellten Aufgaben finden Sie im Kapitel "Hinweise und Lösungen zu den Übungen". Zu jeder Übung wird eine Bearbeitungszeit vorgegeben.