12 Funktionen in Polarkoordinaten

Zum Test

12.1 Theorie

12.1.1 Definition Polarkoordinaten

Jeden Punkt in der Ebene kann man neben den kartesischen Koordinaten auch mit Polarkoordinaten beschreiben. Vor allem für Aufgaben, die sich auf Kreise bzw. Kreisabschnitte beziehen, ist die Arbeit mit Polarkoordinaten vorteilhafter als die Verwendung von kartesischen Koordinaten.

Bei den Polarkoordinaten wird ein Strahl, der vom Ursprung O in Richtung der positiven $x$-Achse ausgeht, als Polarachse bezeichnet. Dann ist jeder Punkt der Ebene eindeutig durch die Strecke $r\mathrm{ }(r>0)$ und den Winkel $\phi$ , den die Strecke $r$ mit der Polarachse bildet, festgelegt. Für $\phi$ gilt $\phi \in [0,\mathrm{2\Pi })$ bzw. $\phi \in$$[\mathrm{0°},\mathrm{360°})$ $\phi$ liegt im „Grundbereich“.

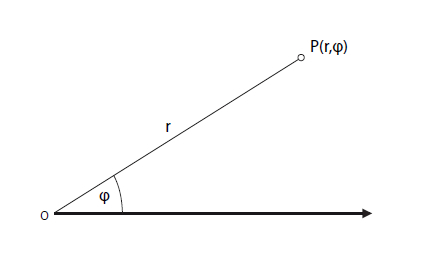
$r$ und $\phi$ sind die Polarkoordinaten eines Punktes der Ebene. Der Winkel kann sowohl in Grad als auch im Bogenmaß angegeben werden.

12.1.2 Beziehungen zwischen kartesischen und Polarkoordinaten

Die Polarkoordinaten lassen sich einfach in die kartesische umrechnen. Es gilt:

${\displaystyle \begin{array}{rcl}x& =& r\cdot \cos \left(\phi \right)\\ y& =& r\cdot \sin \left(\phi \right).\end{array}}$

Bei gegebenen $r$ und $\phi$ sind die kartesischen Koordinaten $x$ und $y$ eindeutig definiert. Umgekehrt gilt:

${\displaystyle \begin{array}{rcl}r& =& \sqrt{x^2+y^2}\\ \tan \phi & =& \frac{y}{x}.\end{array}}$

Dabei ist der Winkel $\phi$ nicht eindeutig definiert. Die Gleichung $\tan \phi =\frac{y}{x}$ hat unendlich viele Lösungen. Sogar wenn man sich auf das Intervall $[0;360)$ beschränkt, gibt es immer noch 2 Lösungen zur Auswahl, die sich um 180° unterscheiden. An dieser Stelle muss man überlegen, in welchem Quadranten der betrachtete Punkt liegt, um sich für einen richtigen Winkel entscheiden zu können.

12.1.3 Kurvengleichungen

Eine Kurve kann als eine Punktmenge aufgefasst werden. Die Vorschrift zur Bildung einer Kurve wird in Form einer Gleichung mit den Variablen $x$ und $y$ (wenn man ein kartesisches Koordinatensystem verwendet) bzw. $r$ und $\phi$ (bei der Verwendung der Polarkoordinaten) angegeben. Ist diese Gleichung nach einer der Variablen aufgelöst, spricht man von einer expliziten Form der Kurvengleichung. Zum Beispiel

${\displaystyle f\left(x\right)=y=x^2.}$

Ist die Gleichung nicht nach einer Variablen aufgelöst, spricht man von einer impliziten Form der Kurvengleichung. Zum Beispiel:

${\displaystyle K(x,y):x^2+y^2-25=0.}$

Mit Hilfe von Polarkoordinaten lassen sich verschiedene Kurvengleichungen darstellen. Zum Beispiel:

• Spiralen:

  ${\displaystyle \begin{array}{rcl}{K}_1& :& r=\phi \\ K_2& :& r=e^{\phi }\\ K_3& :& r={\phi }^{-1}.\end{array}}$

  Folgende Abbildung stellt die Archimedische Spirale $K_1$ für $\phi \ge 0$ dar:

  

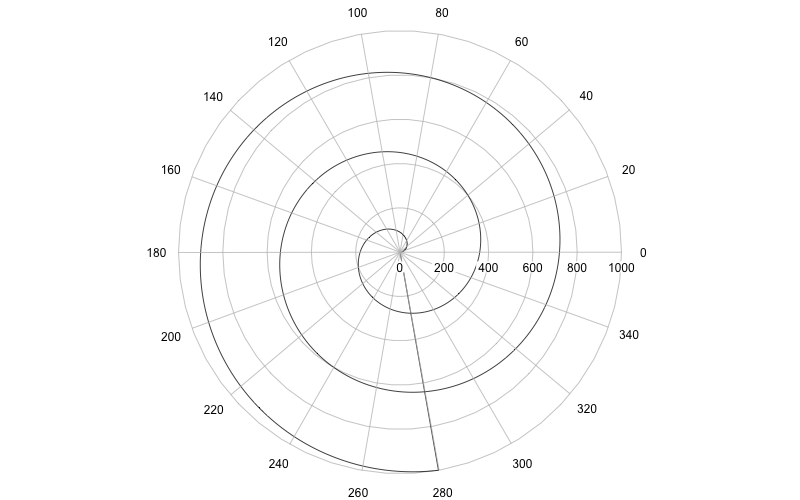
• Kardioiden:

  ${\displaystyle K_4:r=1+\cos \phi .}$
  

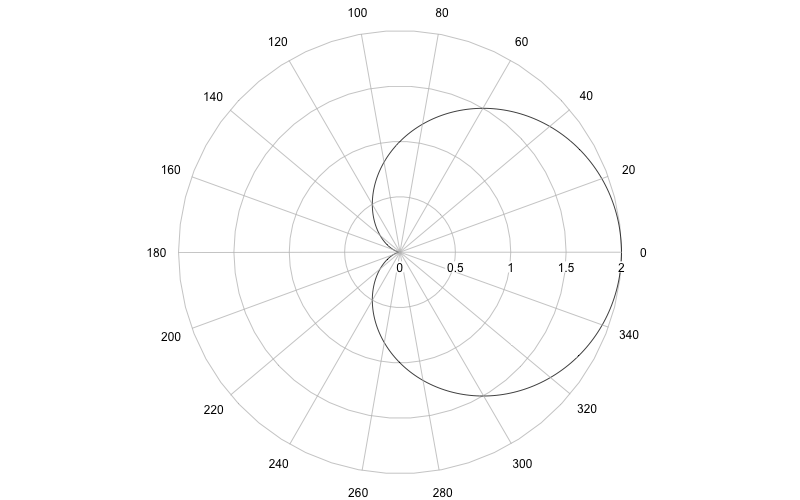
• Lemniskaten:

  ${\displaystyle K_5:r={\cos }^2\phi .}$
  

Die folgenden Videos sollen die theoretischen Erläuterungen unterstützen:

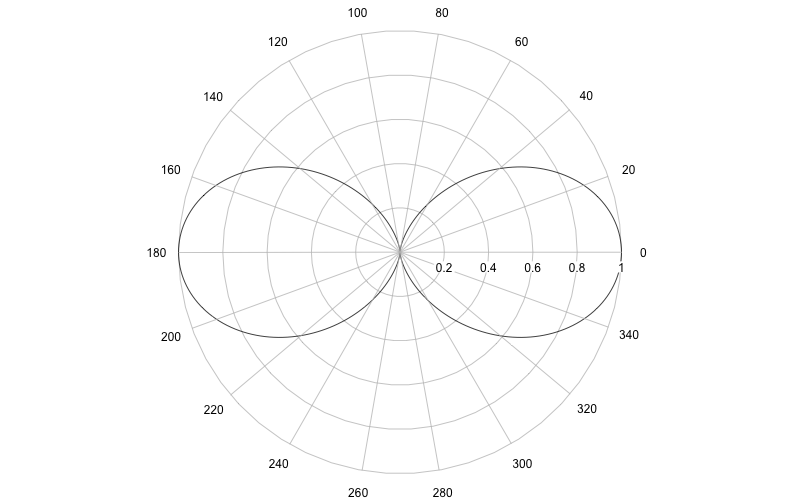
Polarkoordinaten	Funktionen in Polarkoordinaten
Dieses Videos sind Bestandteil des Moodle-Projekts innerhalb der HTW-Berlin.

12.2 Beispiele

Beispiel 12.2.1

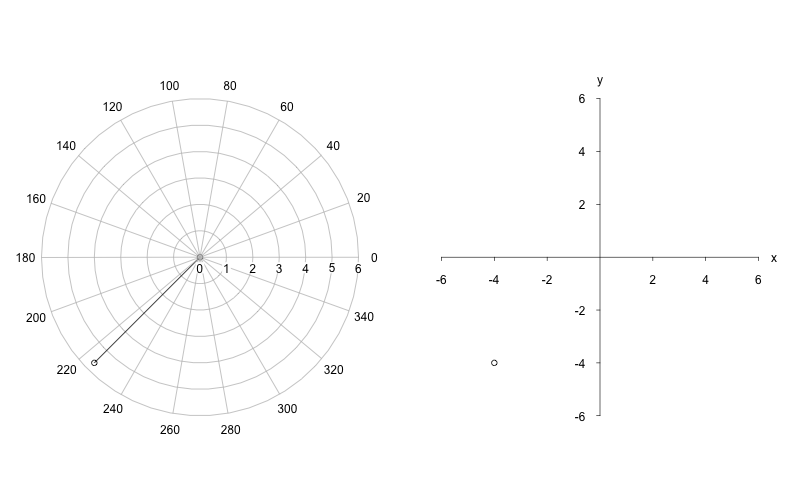
Wie lauten die kartesischen Koordinaten des Punktes $P(4\sqrt{2};{225}^{\circ })$? Prüfen Sie Ihr Ergebnis an einer Skizze nach!

Lösung:

${\displaystyle \begin{array}{rcl}x& =& r\cdot \cos \phi \\ & =& 4\sqrt{2}\cdot \cos \left({225}^{\circ }\right)\\ & =& 4\sqrt{2}\cdot (-\frac{\sqrt{2}}{2})\\ & =& -4\end{array}}$ ${\displaystyle \begin{array}{rcl}y& =& r\cdot \sin \phi \\ & =& 4\sqrt{2}\cdot \sin \left({225}^{\circ }\right)\\ & =& 4\sqrt{2}\cdot (-\frac{\sqrt{2}}{2})\\ & =& -4\end{array}}$

Der Punkt P hat die kartesischen Koordinaten

${\displaystyle P(-4;-4).}$

Beispiel 12.2.2

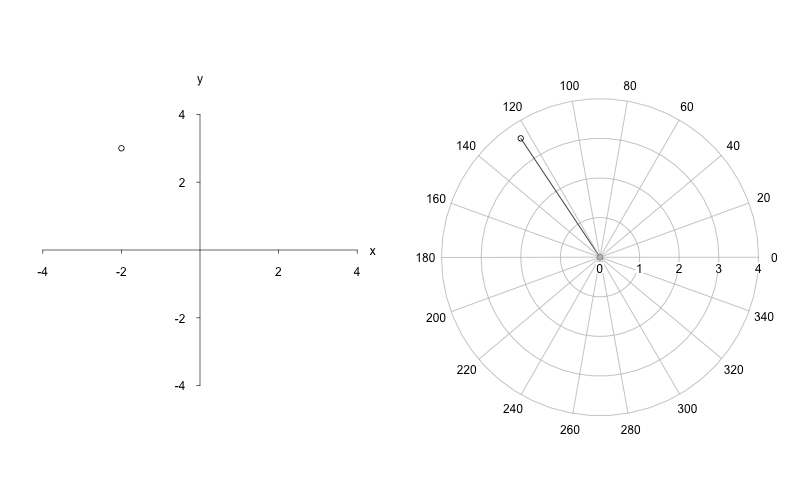
Welche Polarkoordinaten besitzen die Punkte $P(-2;3)$ und? $P(2;-3)$ Prüfen Sie Ihr Ergebnis an einer Skizze nach!

Lösung:

${\displaystyle \begin{array}{rcl}r& =& \sqrt{{(-2)}^2+3^2}\\ & =& \sqrt{13}\\ & \approx & \mathrm{3,61}\end{array}}$ ${\displaystyle \begin{array}{rclll}\tan \phi & =& \frac{3}{-2}& =& -\mathrm{1,5}\end{array}}$

Daraus folgen zwei Winkel

${\phi }_1\approx \mathrm{123,}{69}^{\circ }$

und

${\phi }_2\approx \mathrm{303,}{69}^{\circ }=\; 123,69°\; +\; 180°$.

Da aber der Punkt $P$ im zweiten Quadranten liegt, kommt nur ${\phi }_1$ in Frage. Die Polarkoordinaten des Punktes lauten somit

${\displaystyle P(\sqrt{13};\mathrm{123,}{69}^{\circ }).}$

Beispiel 12.2.3

Ein Kreis mit dem Radius 5 um den Ursprung hat in kartesischen Koordinaten folgende Gleichung:

${\displaystyle K(x,y):x^2+y^2-25=0.}$

Wie lautet diese Kreisgleichung in Polarkoordinaten?

Lösung: Für die Umrechnung der Kurvengleichung wird für $x$ der Ausdruck $r\cdot \cos \phi$ und für $y$ der Ausdruck $r\cdot \sin \phi$ eingesetzt. Man erhält:

${\displaystyle \begin{array}{rcl}{(r\cos \phi )}^2+{(r\sin \phi )}^2-25& =& 0\\ r^2{\cos }^2\phi +r^2{\sin }^2\phi -25& =& 0\\ r^2({\cos }^2\phi +si{n}^2\phi )-25& =& 0.\end{array}}$

Mit ${\sin }^2\phi +{\cos }^2\phi =1$ ergibt sich.

${\displaystyle \begin{array}{rcl}{r}^2-25& =& 0\\ r& =& 5.\end{array}}$

Also lautet die Kreisgleichung

${\displaystyle K:r=5.}$

Beispiel 12.2.4

Wie lautet die Kurvengleichung

${\displaystyle K:r=2\sin \phi }$

in kartesischen Koordinaten?

Lösung: Für $r$ können Sie sofort $\sqrt{x^2+y^2}$ einsetzen:

${\displaystyle \sqrt{x^2+y^2}=2\sin \phi .}$

Weiterhin können Sie aus der Formel $y=r\cdot \sin \phi$ leicht den Ausdruck $\sin \phi$ herleiten:

${\displaystyle \begin{array}{rcl}\sin \phi & =& \frac{y}{r}\\ & =& \frac{y}{\sqrt{x^2+y^2}}.\end{array}}$

Man erhält

${\displaystyle \begin{array}{rcl}\sqrt{x^2+y^2}& =& \frac{\mathrm{2y}}{\sqrt{x^2+y^2}}\\ {\left(\sqrt{x^2+y^2}\right)}^2& =& \mathrm{2y}\\ x^2+y^2& =& \mathrm{2y}\\ x^2+y^2-\mathrm{2y}& =& 0.\end{array}}$

Die Kurvengleichung in kartesischen Koordinaten lautet beispielsweise

${\displaystyle K(x,y):x^2+y^2-\mathrm{2y}=0}$

12.3 Übungsaufgaben

Die Lösungen zu den hier gestellten Aufgaben finden Sie im Kapitel "Hinweise und Lösungen zu den Übungen". Zu jeder Übung wird eine Bearbeitungszeit vorgegeben.

Übung 12.3.1

a)	Welche Polarkoordinaten besitzen die Punkte $A(3;2)$,$\mathrm{ B}(-7;-9)$?
b)	Wie lauten die kartesischen Koordinaten der Punkte $C(5;{30}^{°})$,$\mathrm{ D}(\mathrm{2,5};{270}^{°})$?

Bearbeitungszeit: a) 5 Minuten, b) 5 Minuten

Übung 12.3.2

Wie lautet die folgende Kurvengleichung in Polarkoordinaten?

${\displaystyle K(x;y):{(x^2+y^2)}^2-(x^2-y^2)=0.}$ Bearbeitungszeit: 7 Minuten

Übung 12.3.3

Wie lautet die folgende Kurvengleichung in kartesischen Koordination?

${\displaystyle K:r=\frac{a}{b\cos \phi +c\sin \phi }}$ Bearbeitungszeit: 7 Minuten

Übung 12.3.4

Wie lautet die Kurvengleichung in kartesischen Koordinaten?

${\displaystyle K:r^2=2e^2\cos 2\phi }$ Bearbeitungszeit: 7 Minuten


Zum Test

• Startseite
• Einführung
• Inhaltsverzeichnis
  • 1 Umstellen von Gleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 2 Potenzen und Wurzeln
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 4 Polynomdivision
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 5 Mengenlehre
    • Theorie
  • 6 Funktionen
    • Theorie
  • 7 Lineare Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 8 Quadratische Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 11 Trigonometrische Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 12 Funktionen in Polarkoordinaten
    • Theorie
    • Beispiele
    • Übungen
    • Test
• 13 Hinweise und Lösungen zu den Übungen
  • 1 Umstellen von Gleichungen
  • 2 Potenzen und Wurzeln
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
  • 4 Polynomdivision
  • 7 Lineare Funktionen
  • 8 Quadratische Funktionen
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
  • 11 Trigonometrische Funktionen
  • 12 Funktionen in Polarkoordinaten
• 14 Hinweise und Lösungen zu den Tests
  • 1 Umstellen von Gleichungen
  • 2 Potenzen und Wurzeln
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
  • 4 Polynomdivision
  • 7 Lineare Funktionen
  • 8 Quadratische Funktionen
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
  • 11 Trigonometrische Funktionen
  • 12 Funktionen in Polarkoordinaten