7 Lineare Funktionen

Zum Test

7.1 Theorie

7.1.1 Einleitung

Lineare Funktionen sind Polynome ersten Grades bzw. Geraden der Form $y=a_{1}x+a_0$ . Es werden nur zwei Punkte benötigt, um eine lineare Funktion eindeutig zu bestimmen. Es gibt drei verschiedene Darstellungsformen, dabei ist die Wahl der Formeln abhängig von der Aufgabenstellung:

• Parameterdarstellung
  
  Eine Gerade ist definiert durch einen Anstieg und den Punkt, wo sie die $y$-Achse schneidet, was folgende Formel ausdrückt:

  ${\displaystyle y=mx+n}$

  mit $m$ als Anstieg und $n$ als $y$-Achsenabschnitt.

• Zwei-Punkte-Formel
  
  Eine lineare Funktion kann auch durch zwei Punkte $(x_0;y_0)$ und $(x_1;y_1)$ definiert sein, dann gilt die Gleichung

  ${\displaystyle \frac{y-y_0}{y_1-y_0}=\frac{x-x_0}{x_1-x_0}.}$

• Punktrichtungsformel
  
  Die Punktrichtungsformel berücksichtigt die Steigung und einen beliebigen Punkt $(x_0;y_0)$. Sie lautet

  ${\displaystyle y=m(x-x_0)+y_0.}$

Die Steigung einer Geraden kann leicht durch das Steigungsdreieck ermittelt werden, was durch folgende Formel ausgedrückt wird:

${\displaystyle m=\frac{y_1-y_0}{x_1-x_0}}$

Die lineare Funktion ist eine besonders einfache und wichtige Funktion, für die folgenden (im Kapitel über allgemeine Funktionen vorgestellten) Eigenschaften gelten:

Monotonie:

Deswegen sind lineare Funktionen immer umkehrbar, da es sich immer um streng monoton wachsende oder streng monoton fallende Funktionen handelt.

Symmetrie:

Außerdem sind Geraden keine periodischen Funktionen.

7.1.2 Schnittpunkt von Geraden

Wenn zwei Geraden sich schneiden, nennt man den gemeinsamen Punkt Schnittpunkt. In diesem Punkt wird dem $x$ -Wert von beiden linearen Funktionen der gleiche $y$ -Wert zugeordnet:

${\displaystyle f_1\left(x\right)=y=f_2\left(x\right)}$

Die Ermittlung des Schnittpunktes erfolgt demnach folgendermaßen:

1. Geradengleichungen gleich setzen
2. Nach $x$ auflösen, um die Schnittstelle zu erhalten
3. Den berechneten $x$-Wert in eine der zwei Gleichungen einsetzen, um den $y$-Wert zu bestimmen.

In den vorgerechneten Beispielen dieses Kapitels wird noch die Vorgehensweise an einem konkreten Beispiel erläutert.

7.1.3 Orthogonale Geraden

Zwei Geraden nennt man orthogonal, wenn sie sich in einem rechten Winkel schneiden. Für die Steigungen und orthogonaler Geraden gilt

${\displaystyle m_1\cdot m_2=-1.}$

Mit Hilfe dieser Gleichung kann man Geraden auf Orthogonalität prüfen oder eine orthogonale Gerade zu einer anderen Geraden bestimmen.

7.1.4 Abstand eines Punktes zu einer Geraden

Mit Abstand bezeichnet man immer den kürzesten Abstand $d$ zwischen einem Punkt $P$ und der Geraden $y=mx+n$. Dieser ist in der Abbildung durchgehend schwarz gekennzeichnet.

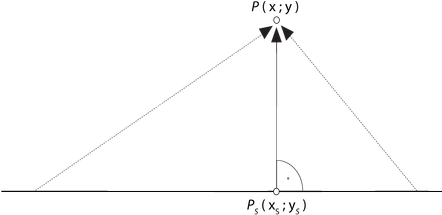
Der Punkt $P$ liegt also auf einer orthogonalen Geraden, die bei der Berechnung hilfreich sein wird.

Der Abstand wird wie folgt berechnet:

1. Berechnung einer orthogonalen Hilfsgeraden, die durch $P$ verläuft und orthogonal zu der gegebenen Geraden ist. Dies bezeichnet man auch als “Fällen eines Lots” von Punkt $P$ auf die Gerade.
2. Bestimmung des Schnittpunktes $P_{\mathrm{S}}$ der Geraden und der orthogonalen Hilfsgeraden.

3. Den Abstand $d$ zwischen dem Punkt $P$ und dem Schnittpunkt $P_{\mathrm{S}}$ bzw. die Länge des Lots berechnet man mit der folgenden Formel, die auf dem Satz des Pythagoras basiert:

   ${\displaystyle \mathrm{d\; =}\sqrt{{(x-x_{\mathrm{s}})}^2+{(y-y_{\mathrm{s}})}^2}}$

7.1.5 Betragsfunktion

Die Betragsfunktion $f\left(x\right)=|x|$ ordnet jedem Wert $x$ dessen Absolutbetrag zu. Dieser ist definiert durch

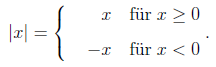
Die Grafik zeigt beispielhaft die Funktion $f\left(x\right)=|x|$:

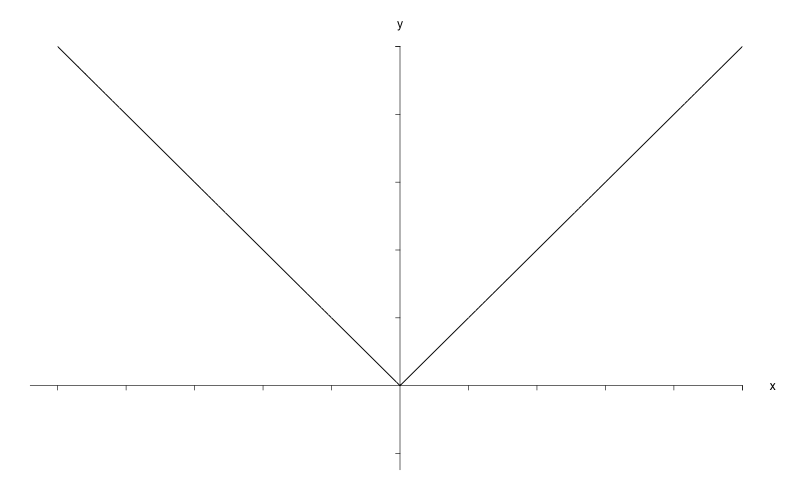
Die Funktion ist für $x\le 0$ streng monoton fallend und wächst streng monoton für $x\ge 0$. Im Punkt $(0;0)$ nimmt die Betragsfunktion ein Minimum an, ist an dieser Stelle jedoch nicht differenzierbar.

Bitte beachten Sie, dass nicht nur Betragsfunktionen basierend auf linearen Funktionen existieren. Es gibt z.B. auch Betragsfunktionen der Form $f\left(x\right)=|x^2-4|$,  $f\left(x\right)=|\sin x|$ oder $f\left(x\right)=|\ln x|+1$.

Betragfunktionen

Dieses Video ist Bestandteil des Moodle-Projekts innerhalb der HTW Berlin.

7.1.6 Lineare Ungleichungen

Ungleichungen verknüpfen Variablen nicht durch das Gleichheitszeichen sondern durch die Zeichen $<,\le ,>$ und $\ge$ ; so z.B. die Ungleichung $x+3>4x+2$ . In diesem Fall ist von Interesse, welche Werte für die Variable $x$ aus dieser Ungleichung eine wahre Aussage liefern. Diese x-Werte bilden die Lösungsmenge der gegebenen Ungleichung. Lineare Ungleichungen sind besonders einfach, da nur Fallunterscheidung vorgenommen werden müssen, wenn neben der einen Variablen auch Parameter vorkommen. Ungleichungen können zeichnerisch gelöst werden, was anhand der Beispiele noch näher erläutert wird. Bei der rechnerischen Lösung wird die Lösungsmenge durch Umstellen nach x ermittelt. Der Lösungsbereich wird mit einer geeigneten Schreibweise für Mengen dargestellt.

Die Sachverhalte werden nun an Beispielen erläutert.

7.2 Beispiele

Beispiel 7.2.1

Zeichnen Sie die Funktionen und bestimmen Sie die Geradengleichung anhand der gegebenen Angaben

1.)	$P_1(4;3)$	$P_2(1;2)$
2.)	$P_1(2;0)$	$m=3$
3.)	$n=1$	$m=0$

Die Sachverhalte dieses Kapitels werden nun an Beispielen noch einmal erläutert.

Rechnerische Lösung:

1.) Da zur Aufstellung der Geraden zwei Punkte angegeben sind, bietet es sich an, die Zwei-Punkte-Formel zu verwenden:

${\displaystyle \frac{y-3}{2-3}=\frac{x-4}{1-4}}$

Diese Formel kann man durch Umstellen leicht in die Parameterform, die für weitere Berechnungen geeigneter ist, überführen:

${\displaystyle \begin{array}{rcl}\frac{y-3}{-1}& =& \frac{x-4}{-3}\\ -3(y-3)& =& -1(x-4)\\ -3y+9& =& -x+4\\ -3y& =& -x-5\\ y& =& \frac{1}{3}x+\frac{5}{3}\end{array}}$

2.) Für dieses Beispiel bietet sich die Punktrichtungsformel an:

${\displaystyle \begin{array}{rclll}y& =& 3(x-2)+0& =& 3x-6\end{array}}$

3.) Die Angaben können direkt in die Parameterdarstellung übernommen werden:

${\displaystyle \begin{array}{rclll}y& =& 0\cdot x+1& =& 1\end{array}}$

Grafische Lösung:

1.) Die Gerade lässt sich schnell zeichnen, indem man die zwei gegebenen Punkte einträgt und diese miteinander verbindet.

2.) Die Gerade kann gezeichnet werden, indem man das Wissen über die Parameter aus dem Kapitel über allgemeine Funktionseigenschaften anwendet. Alternativ kann man auch das Steigungsdreieck verwenden.

3.) Hier handelt es sich um eine spezielle Gerade, die parallel zur $x$-Achse durch $y=1$ verläuft.

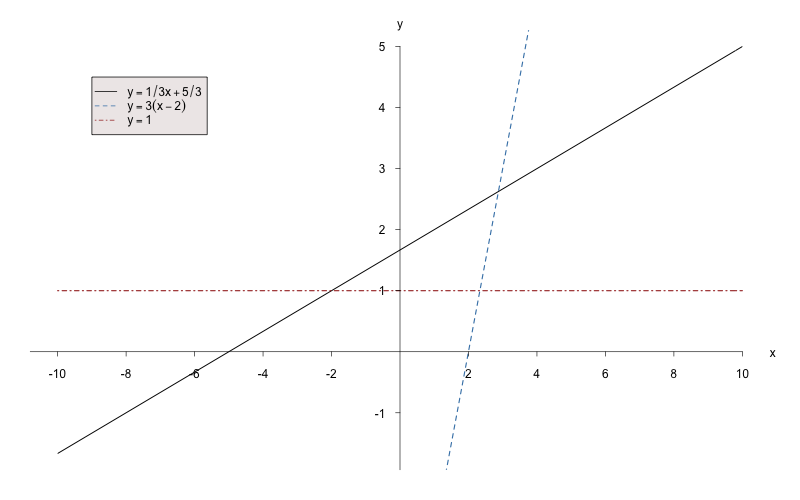
Beispiel 7.2.2

Bestimmen Sie den Schnittpunkt zwischen der Geraden aus Beispiel 7.2.1 (1.) und $f\left(x\right)=2x$.

Lösung: Der Schnittpunkt wird durch Gleichsetzen der beiden linearen Funktionen berechnet:

${\displaystyle \frac{1}{3}x+\frac{5}{3}=2x}$

Nun wird diese Gleichung nach $x$ aufgelöst:

${\displaystyle \begin{array}{rcl}\frac{5}{3}& =& 2x-\frac{1}{3}x\\ \frac{5}{3}& =& \frac{6}{3}x-\frac{1}{3}x\\ \frac{5}{3}& =& \frac{5}{3}x\\ x& =& 1\end{array}}$

Um den $y$-Wert zu ermitteln, muss der $x$-Wert des Schnittpunktes in eine der beiden Funktionen eingesetzt werden:

${\displaystyle \begin{array}{rclll}y& =& 2\cdot 1& =& 2\end{array}}$

Der Schnittpunkt beider Geraden lautet somit $S(1;2)$.

Beispiel 7.2.3

Berechnen Sie den Abstand der Geraden aus Beispiel 7.2.1 (1.) zu dem Punkt $P(4;5)$.

Lösung: Um diese Übung zu lösen, wird zunächst der Anstieg der orthogonalen Hilfsgeraden bestimmt:

${\displaystyle \begin{array}{rcl}{m}_1\cdot m_H& =& -1 \wedge m_1=\frac{1}{3}\\ m_H& =& \frac{-1}{\frac{1}{3}}\\ m_H& =& -3\end{array}}$

Da für die Hilfsgerade der Punkt $P(4;5)$ und der Anstieg $m_H=-3$ gegeben sind, kann nun leicht die Punktrichtungsformel angewendet werden:

${\displaystyle y=-3(x-4)+5.}$

Für die Berechnung des Schnittpunktes ist die Parameterform besser geeignet. Deshalb sollte man die Gleichung gleich ausmultiplizieren:

${\displaystyle \begin{array}{rclll}y& =& -3x+12+5& =& -3x+17.\end{array}}$

Anschließend wird der Schnittpunkt beider Geraden (durch Gleichsetzen) bestimmt:

${\displaystyle \frac{1}{3}x+\frac{5}{3}=-3x+17.}$

Nun wird nach $x$ aufgelöst:

${\displaystyle \begin{array}{rcl}\frac{1}{3}x+3x& =& 17-\frac{5}{3}\\ \frac{1}{3}x+\frac{9}{3}x& =& \frac{51}{3}-\frac{5}{3}\\ \frac{10}{3}x& =& \frac{46}{3}\\ x& =& \frac{46}{10}\\ x& =& \frac{23}{5}.\end{array}}$

Der $y$-Wert des Schnittpunktes wird ermittelt indem man den $x$-Wert in eine der Geradengleichungen einsetzt:

${\displaystyle \begin{array}{rclll}y& =& -3\cdot \frac{23}{5}+17& =& \frac{16}{5}.\end{array}}$

Der Schnittpunkt lautet also $S_H(\frac{23}{5};\frac{16}{5})$.

Es wird nun der Abstand zwischen den Punkten $P(4;5)$ und $S_H(\frac{23}{5};\frac{16}{5})$ mit der oben erläuterten Formel berechnet:

${\displaystyle \begin{array}{rcl}d& =& \sqrt{{(4-\frac{23}{5})}^2+{(5-\frac{16}{5})}^2}\\ d& =& \sqrt{{(\frac{20}{5}-\frac{23}{5})}^2+(\frac{25}{5}-\frac{16}{5})}\\ d& =& \sqrt{{(-\frac{3}{5})}^2+{\left(\frac{9}{5}\right)}^2}\\ d& =& \sqrt{\frac{9}{25}+\frac{81}{25}}\\ d& =& \sqrt{\frac{90}{25}}\\ d& =& \frac{\sqrt{90}}{5}\\ d& =& \frac{3\cdot \sqrt{10}}{5}.\end{array}}$

Der kürzeste Abstand zwischen dem Punkt $P(4;5)$ und der Geraden beträgt $\frac{3\sqrt{10}}{5}$.

Beispiel 7.2.4

Zeichnen Sie die folgenden Funktionen:

${\displaystyle \begin{array}{rcl}\text{a)}f\left(x\right)& =& 2(x+1)-3\\ \text{b)}f\left(x\right)& =& 3|x-2|-1\end{array}}$

Hinweis: Zeichnen Sie zuerst die Funktion $f\left(x\right)=x$ bzw. $f\left(x\right)=|x|$ und verschieben, spiegeln und stauchen Sie diese Funktion mit Hilfe der Parameterangaben. Die Bedeutung der einzelnen Parameter können Sie im Kapitel über die allgemeinen Funktionseigenschaften nachlesen.

Lösung:

a) Es handelt sich um die lineare Funktion $f\left(x\right)=x$, die

• um $1$ nach links verschoben wird,
• gestreckt wird in $y$-Richtung (bzw. deren Steigung sich von $m=1$ auf $m=2$ erhöht) und
• um $3$ nach unten verschoben wird.

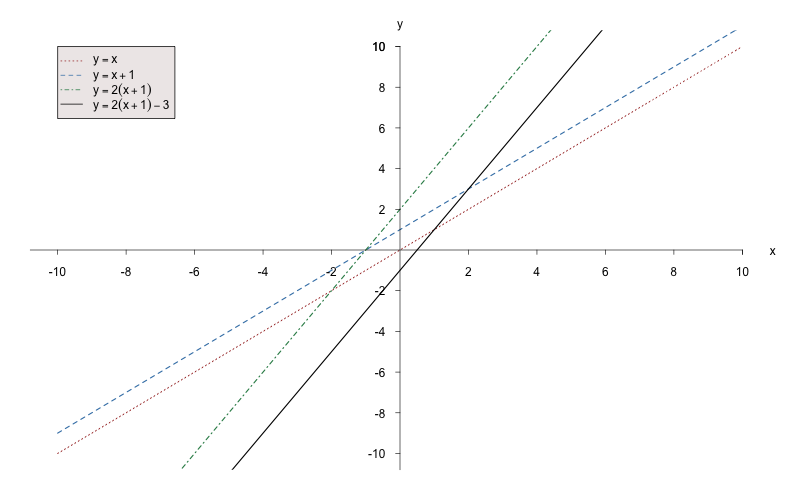
b) Es handelt sich um eine Betragsfunktion, die

• um $2$ nach rechts verschoben wird,
• gestreckt wird in $y$-Richtung und
• um $1$ nach unten verschoben wird.

Beispiel 7.2.5

Lösen Sie folgende Ungleichungen und diskutieren Sie deren grafische Bedeutung.

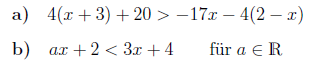
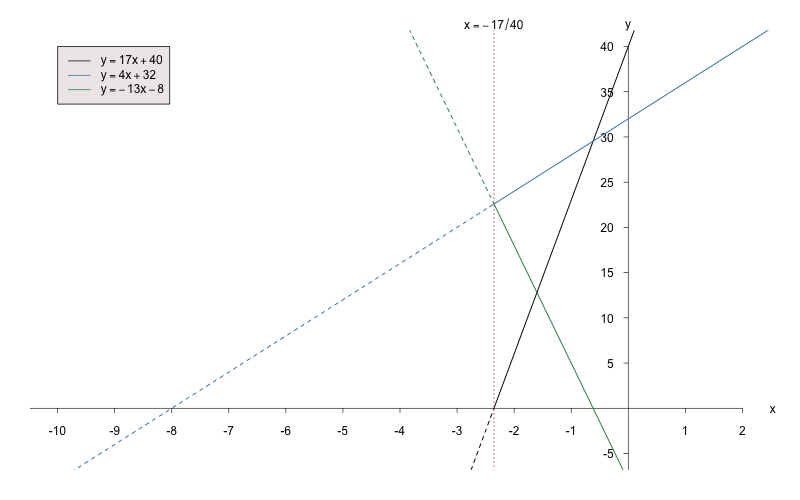
Lösung: Beide Aufgaben sollen zunächst rechnerisch, Teil a) anschließend auch grafisch ausgewertet werden.

a) Zuerst wird ausmultipliziert:

${\displaystyle 4x+12+20>-17x-8+4x}$

Dann kann die Ungleichung so umgestellt werden, dass $x$ auf einer Seite isoliert ist:

${\displaystyle \begin{array}{rcl}4x+17x-4x& >& -8-12-20\\ 17x& >& -40\end{array}}$

Nun sollte das Ergebnis noch in Mengenschreibweise formuliert werden:

${\displaystyle L=\{x|x>-\frac{40}{17}\}}$

Grafisch kann man sich unter der Ungleichung $17x>-40$ bzw. $17x+40>0$ vorstellen, für welche $x$ die Funktion$17x+40$ positiv ist (schwarz dargestellt). Oder aber man überlegt, ab welcher Stelle $x$ die Funktion $4x+12+20$ größere Funktionswerte annimmt als die Funktion $17x-8+4x$ (farbig dargestellt) :

b) Das besondere an dieser Gleichung ist, dass $a$ unbekannt ist. Deswegen muss eine Fallunterscheidung vorgenommen werden.

Zunächst wird die Ungleichung wieder nach $x$ umgestellt:

${\displaystyle \begin{array}{rcl}ax-3x& <& 4-2\\ (a-3)x& <& 4-2\end{array}}$

Nun muss durch $(a-3)$ dividiert werden. Dabei ist zu beachten, dass für diesen Schritt $a\ne 3$ sein muss. Wenn $(a-3)>0$ ist, bleibt das Verhältniszeichen “$<$”. Sollte $(a-3)<0$ sein, so muss es umgekehrt werden, also wird “$<$” zu “$>$” geändert. Anschließend erfolgt die Unterscheidung der verschiedenen möglichen Fälle:

1. Fall: $a=3$

${\displaystyle \begin{array}{rcl}(3-3)x& <& 2\\ 0& <& 2\end{array}}$

wahre Aussage, damit ist $\mathrm{𝕃}=\mathrm{ℝ}$

2. Fall: $a-3<0$

${\displaystyle x<\frac{2}{a-3}}$
Die Lösungsmenge ist $\mathrm{𝕃}=\{ x | x < \frac{2}{a-3}, a>3\}$

3. Fall: $a-3>0$

${\displaystyle x>\frac{2}{a-3}}$
Lösungsmenge: $\mathrm{𝕃}=\{ x | x > \frac{2}{a-3}, a<3\}$

Zusammenfassen kann man das Ergebnis aller Fälle durch folgende Lösungsmenge:

 

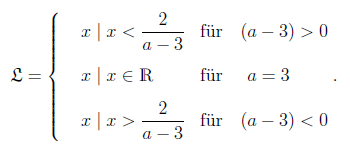
Die folgenden Pencasts erläutern ausführlich zwei weitere Beispiele:

7.3 Übungen

Die Lösungen zu den hier gestellten Aufgaben finden Sie im Kapitel "Hinweise und Lösungen zu den Übungen". Zu jeder Übung wird eine Bearbeitungszeit vorgegeben.

Übung 7.3.1

Berechnen Sie die Geradengleichung und zeichnen Sie die Funktion, falls gegeben sind:

Bearbeitungszeit: a) 5 Minuten, b) 5 Minuten, c) 7 Minuten

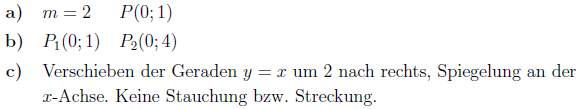
Übung 7.3.2

a) Bestimmen Sie die orthogonale Gerade zur Funktion $y=4x-2$, die durch den Punkt $P_1(0;3)$ verläuft.

b) Bestimmen Sie den Schnittpunkt der Geraden:

${\displaystyle \begin{array}{rclllll}{y}_1& =& 4x-2& \text{ und }& y_2& =& -\frac{1}{4}x+3\end{array}}$

c) Berechnen Sie den Abstand der Punkte $P_1(0;3)$ und $P_2(\frac{20}{17};\frac{46}{17})$ .

Bearbeitungszeit: a) 4 Minuten, b) 6 Minuten, c) 8 Minuten

Übung 7.3.3

Berechnen Sie die Lösungsmenge folgender Ungleichungen und stellen Sie das Problem aus Übung a) grafisch dar.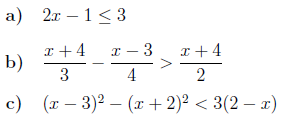

Bearbeitungszeit: a) 4 Minuten, b) 8 Minuten, c) 10 Minuten

Übung 7.3.4

Berechnen Sie jeweils die Lösungsmenge folgender Ungleichungen. Bitte beachten Sie dabei, dass Fallunterscheidungen notwendig sind.

Bearbeitungszeit: a) 10 Minuten, b) 12 Minuten

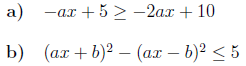
Zum Test

• Startseite
• Einführung
• Inhaltsverzeichnis
  • 1 Umstellen von Gleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 2 Potenzen und Wurzeln
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 4 Polynomdivision
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 5 Mengenlehre
    • Theorie
  • 6 Funktionen
    • Theorie
  • 7 Lineare Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 8 Quadratische Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 11 Trigonometrische Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 12 Funktionen in Polarkoordinaten
    • Theorie
    • Beispiele
    • Übungen
    • Test
• 13 Hinweise und Lösungen zu den Übungen
  • 1 Umstellen von Gleichungen
  • 2 Potenzen und Wurzeln
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
  • 4 Polynomdivision
  • 7 Lineare Funktionen
  • 8 Quadratische Funktionen
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
  • 11 Trigonometrische Funktionen
  • 12 Funktionen in Polarkoordinaten
• 14 Hinweise und Lösungen zu den Tests
  • 1 Umstellen von Gleichungen
  • 2 Potenzen und Wurzeln
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
  • 4 Polynomdivision
  • 7 Lineare Funktionen
  • 8 Quadratische Funktionen
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
  • 11 Trigonometrische Funktionen
  • 12 Funktionen in Polarkoordinaten