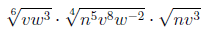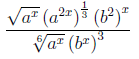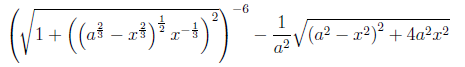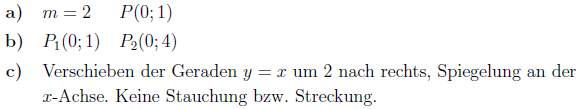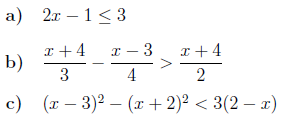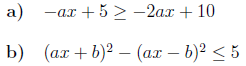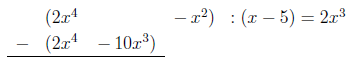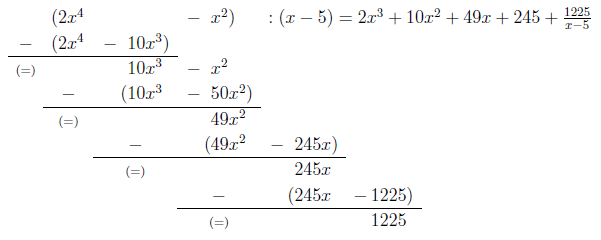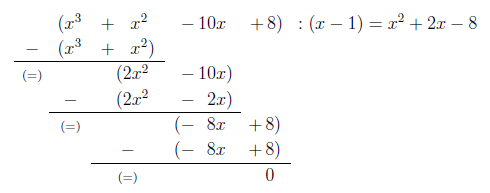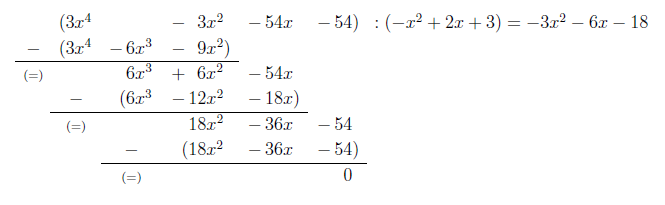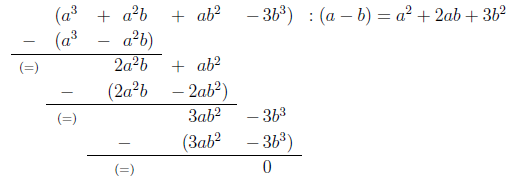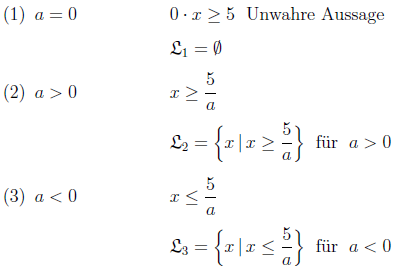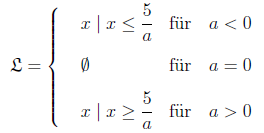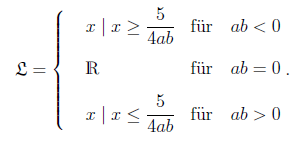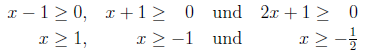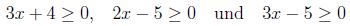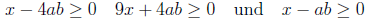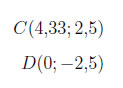13 Hinweise und Lösungen zu den Übungen
In diesem Kapitel sind alle Lösungen der Übungen zu finden.
Sollten Sie weitere Fragen haben, bin ich über Skype unter dem Kontakt "Joachim.Siegert2" zu finden.
13.1 Umstellen von Gleichungen
Übung 1.3.1
Stellen Sie bitte nach
um!
Um leichter nach
umstellen
zu können, empfiehlt es sich, die Gleichung so umzuformen, dass
im Zähler steht:
Bringen Sie alle Terme, in denen
nicht vorkommt, auf die andere Seite der Gleichung:
Es ist immer ratsam, die Terme so weit wie möglich zu
vereinfachen (in diesem Fall durch Bilden des Hauptnenners).
Schließlich muss noch durch
dividiert werden:
Übung 1.3.2
Vereinfachen Sie bitte folgenden
Doppelbruch:
Formen Sie die Summen in den Nennern zu Produkten um, indem
Sie die jeweils
mit
erweitern:
Vereinfachen lässt sich dieser Ausdruck, indem man den
Doppelbruch im Zähler eliminiert durch Multiplikation mit dem
Kehrwert des Nenners (siehe Division von Brüchen im Theorieteil):
Beseitigen Sie nun den letzten Doppelbruch und fassen Sie
schließlich das Ergebnis zusammen:
Übung 1.3.3
Stellen Sie folgende Gleichung nach
um:
Klammern Sie nun
aus, damit
nur noch an einer Stelle in der Gleichung steht:
Nun müssen Sie nur noch durch den Term dividieren, der
als Faktor vor
auftritt und anschließend die Doppelbrüche beseitigen:
Übung 1.3.4
Stellen Sie folgende Gleichung nach
um:
Wieder sollte die Gleichung so umgestellt werden, dass
nur an einer Stelle in der Gleichung steht. Dazu sollten Sie
zunächst die Brüche beseitigen:
Sortieren Sie nun die Gleichung, indem Sie alle Terme mit
auf eine Seite bringen:
Klammern Sie anschließend
sowie
aus:
Die Gleichung kann nun leicht umgestellt und vereinfacht
werden:
13.2 Potenzen und Wurzeln
Übung 2.3.1
Vereinfachen Sie so weit wie möglich:
Wenden Sie das Gesetz über die Division bzw.
Multiplikation von Potenzen mit gleichen Exponenten an. Dann ergibt sich
folgender Ausdruck:
Nun kann das Gesetz über das Potenzieren von Potenzen
verwendet werden, um den Ausdruck später zu vereinfachen:
Die Terme können nun leicht multipliziert werden
Wenn nötig sollte der Bruch nun wieder sortiert
werden, um anschließend die Gesetze für Potenzen mit gleicher
Basis anzuwenden:
Übung 2.3.2
Vereinfachen Sie bitte folgenden Ausdruck:
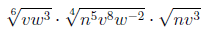
Schreiben Sie die Wurzeln als Exponenten um:
Da die Wurzeln gleiche Exponenten für verschiedene
Basen sind, kann der Ausdruck umgeformt werden zu:
Nun können die doppelten Potenzen zu einfachen
Potenzen vereinfacht werden:
Fassen Sie nun die Ausdrücke zusammen, indem Sie das
Gesetz zur Multiplikation von Potenzen mit gleicher Basis verwenden:
Übung 2.3.3
Vereinfachen Sie bitte folgenden Ausdruck:
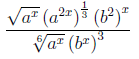
Schreiben Sie den Ausdruck so um, dass jede Basis nur einen
Exponenten hat:
Nun kann die Anwendung der Gesetze für gleiche Basis
erfolgen:
Übung 3.3.1
Bitte berechnen Sie den
Binomialkoeffizienten
.
Wenden Sie die Definition des Binomialkoeffizienten an:
Nutzen Sie die Definition der Fakultät um kürzen
zu können:
Kürzen Sie soweit wie möglich. Beachten Sie
dabei, dass ein Teil des Zählers im Nenner enthalten ist.
Übung 3.3.2
Bestimmen Sie eine Formel für
mit Hilfe des binomischen Lehrsatzes.
Wenden Sie die Definition des binomischen Lehrsatzes an:
Schreiben Sie die Summanden einzeln auf:
Übung 3.3.3
Vereinfachen Sie folgenden Ausdruck so
weit wie möglich:
Gestalten Sie die Nenner einfacher, indem Sie z.B.
Variablen ausklammern und die Nenner als Produkte darstellen.
Kürzen Sie sofern möglich:
Versuchen Sie den zweiten Summanden zu vereinfachen, indem
Sie ausklammern und kürzen. Vergleichen Sie dafür, wo
ähnliche Ausdrücke im zweiten Summanden enthalten sind:
Machen Sie die Brüche gleichnamig. Beachten Sie dabei,
dass der Nenner des zweiten Terms schon fast mit einem Teil des ersten
Terms übereinstimmt:
Führen Sie die Rechenoperationen aus und vereinfachen
Sie so weit wie möglich:
Übung 3.3.4
Vereinfachen Sie den Ausdruck so weit wie
möglich:
Um einen geeigneten Nenner zu finden, wendet man die
Gesetze für binomische Formeln an und formt die Nenner entsprechend
um:
Nun können die Brüche gleichnamig gemacht werden,
um die Zähler zu addieren bzw. subtrahieren.
In Teilen des Zählers kann nun
ausgeklammert werden:
Multiplizieren Sie im Zähler in keinem Fall aus!
Die letzte Klammer des Zählers ergibt ,
wenn man die dritte binomische Formel anwendet:
Anschließend muss nur noch gekürzt werden.
Übung 3.3.5
Vereinfachen Sie folgenden Ausdruck:
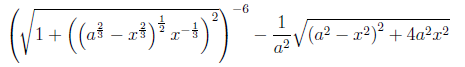
Verwenden Sie Ihr erworbenes Wissen über Potenzen und
Wurzeln. Der erste Ausdruck lässt sich durch Ausmultiplizieren und
der zweite durch Anwenden der binomischen Formeln vereinfachen:
Benutzen Sie für den zweiten Term die Umkehrung der
binomischen Formeln und wenden Sie weiter Potenzgesetze an:
Der erste Term kann weiter nur durch Potenzgesetze
vereinfacht werden. Um den zweiten Term vom ersten zu subtrahieren,
sollte man zuerst den zweiten Term ausmultiplizieren, falls dies noch
nicht geschehen ist:
13.4 Polynomdivision
Übung 4.3.1
Lösen Sie folgende Übung:
Da die Polynome bereits sortiert sind, können Sie
direkt mit der Division beginnen. Dividieren Sie
durch
und multiplizieren Sie das Ergebnis
mit dem Divisor. Achten Sie von Anfang an darauf, Potenzen mit gleichem
Exponenten unter einander zu schreiben. Dies erleichtert später die
Übersicht:
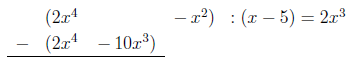
Ermitteln Sie den entstehenden Rest, der noch dividiert
werden muss und führen Sie das Verfahren erneut aus.
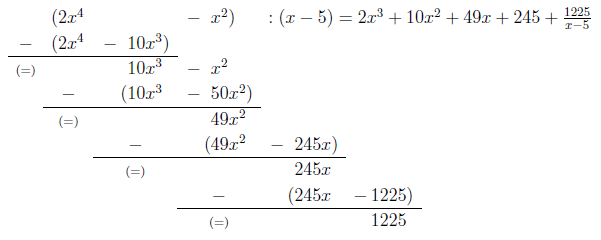
Übung 4.3.2
Berechnen Sie alle Nullstellen des
Polynoms
Ermitteln Sie eine Nullstelle. Meist ist das Absolutglied (
in diesem Fall 8 ) ein Vielfaches der Nullstellen. Eine Möglichkeit
wäre die Zahl 1, da .
Die Probe ergibt: .
ist also eine geeignete Nullstelle.
Dividieren Sie nun das Polynom durch
und fahren Sie mit der Polynomdivision fort:
Ermitteln Sie das erste Glied des Ergebnisses, indem Sie
durch
dividieren und multiplizieren Sie dieses mit dem Divisor:
Ermitteln Sie den Rest und dividieren Sie diesen wie unter
dem vorherigen Tipp beschrieben. Setzen Sie diese Schritte solange fort,
bis kein teilbarer Rest mehr übrig bleibt.
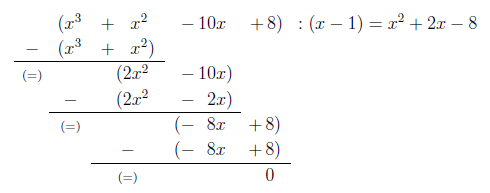
Berechnen Sie nun die anderen Nullstellen, indem Sie die p-q-Formel
für
anwenden:
Übung 4.3.3
Führen Sie die folgende Division aus:
Sortieren Sie zunächst den Divisor entsprechend der
Exponenten (größte Potenz zuerst). Dividieren Sie dann
durch
.
Lassen Sie sich nicht davon irritieren, dass der Divisor drei Glieder
hat, sondern gehen Sie wie gewohnt vor. Ermitteln Sie dann den Rest und
wiederholen Sie das Verfahren so oft wie nötig.
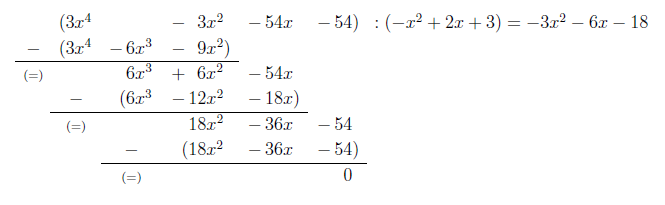
Übung 4.3.4
Lösen Sie bitte folgende
Polynomdivision:
Sortieren Sie nach Variable und Potenz. Dann erhalten Sie:
Teilen Sie
durch
und multiplizieren Sie das Ergebnis
mit dem Divisor und ermitteln Sie den Rest. Ermitteln Sie dann den Rest
und gehen Sie schließlich in gewohnter Weise erneut so vor.
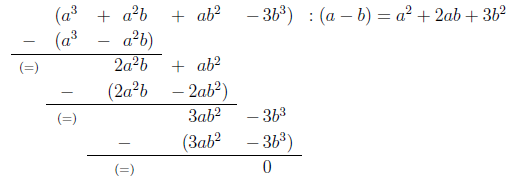
13.7 Lineare Funktionen
Übung 7.3.1
Berechnen Sie die Geradengleichungen und zeichnen Sie die Funktionen.
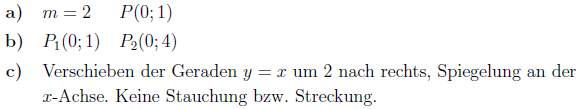 a)
a)
Verwenden Sie eine geeignetet
Formel, die die gegebenen Angaben berücksichtigt:
Setzen Sie die Angaben in die Formel ein:
b)
Kontrollieren Sie
zunächst, ob die Zuordnung der Punkte die Definition einer Funktion
erfüllen kann.
Es handelt sich um keine Funktion, da dem -Wert
unendlich viele (anstatt einem
eindeutigen) -Werte zugeordnet werden.
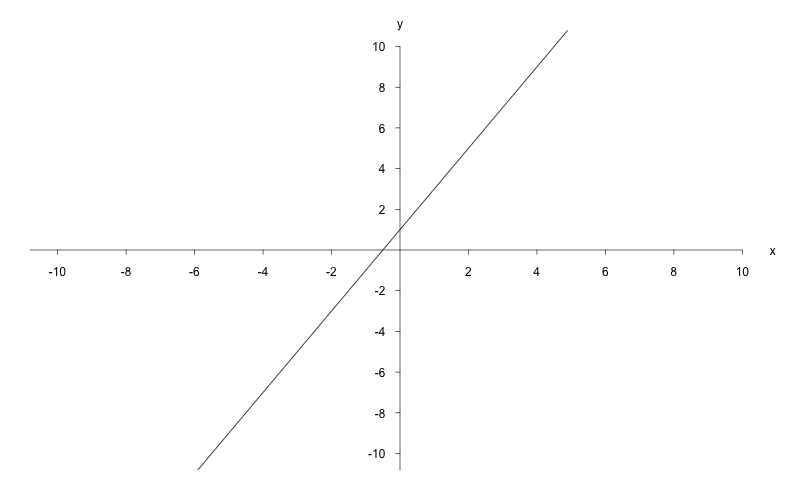
c)
Stellen Sie zuerst eine
Funktionsgleichung auf, die die Gerade
um
verschiebt. Die Wirkung der einzelnen
Parameter kann im Kapitel über die allgemeinen
Funktionseigenschaften nachgelesen werden. Diese Funktion lautet:
Der Parameter
in einer
Funktion
sorgt für eine Spiegelung an der -Achse.
Die gesuchte Funktion hat also die Form
Da angegeben ist, dass die Spiegelung ohne Stauchung bzw.
Streckung erfolgen soll, kann
leicht
bestimmt werden. Somit ist .
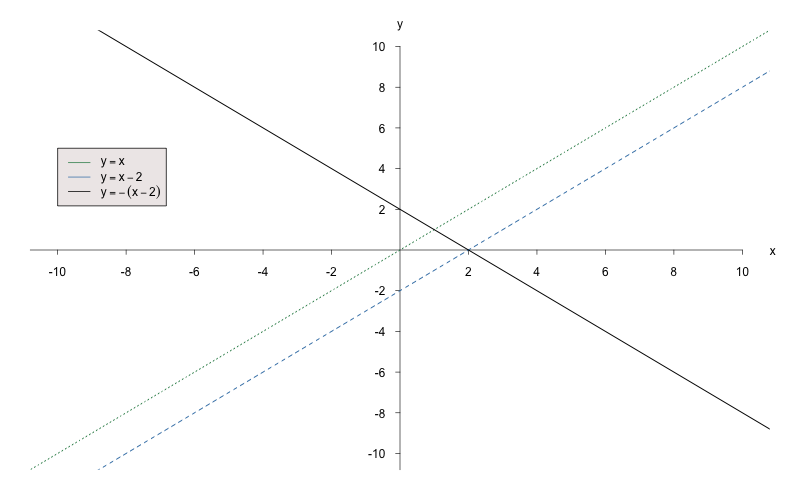
Übung 7.3.2
a)
Bestimmen Sie die orthogonale Gerade zur Funktion ,
die durch den Punkt
verläuft.
b)
Bestimmen Sie den Schnittpunkt der Geraden:
c)
Berechnen Sie den Abstand der Punkte
und
.
a)
Berechnen Sie den Anstieg der gesuchten Geraden
mit Hilfe der Formel
Verwenden Sie nun die Formel, die eine Gerade durch die
Steigung und einen Punkt definiert:
b)
Setzen Sie die Funktionsgleichungen gleich:
Lösen Sie die Gleichung nach
auf:
Setzen Sie den -Wert in eine
Gleichung ein, um den -Wert zu berechnen:
Der Schnittpunkt lautet
c)
Verwenden Sie die Abstandsformel
Setzen Sie nun die nötigen Angaben in die Formel ein:
Der Abstand zwischen den Punkten beträgt
Hinweis:
Durch die Aufgaben a) bis c) haben Sie zugleich den
Abstand zwischen dem Punkt
und der Geraden
berechnet.
Übung 7.3.3
Berechnen Sie die Lösungsmenge
folgender Ungleichungen und stellen Sie das Problem aus Übung a)
grafisch dar.
 a)
a)
Stellen Sie zunächst die Ungleichung nach
um:
Formulieren Sie nun das Ergebnis in Mengenschreibweise.
Es wurde also untersucht, für welchen Definitionsbereich die
Funktion
kleiner oder gleich dem -Wert 3 ist.
Dieser Sachverhalt wird auch in der Grafik dargestellt:
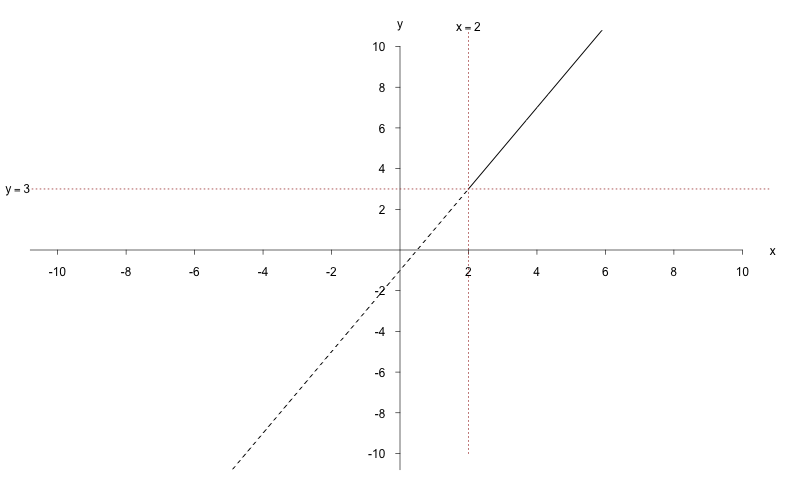
b)
Beseitigen Sie zuerst die Brüche:
Stellen Sie nun die Ungleichung nach
um:
Hinweis:
Bitte beachten Sie, dass das Multiplizieren bzw.
Dividieren mit einer negativen Zahl zu einer Umkehrung des
Verhältniszeichens führt. Somit ergibt sich
Stellen Sie das Ergebnis nun in Mengenschreibweise dar.
c)
Verwenden Sie die binomischen Formeln und fassen
Sie dann die Ausdrücke zusammen:
Stellen Sie die Ungleichung nach
um.
Notieren Sie die Lösung in Mengenschreibweise.
Übung 7.3.4
Berechnen Sie jeweils die
Lösungsmenge folgender Ungleichungen. Bitte beachten Sie dabei,
dass Fallunterscheidungen notwendig sind.
 a)
a)
Fassen Sie die Terme mit
auf einer Seite zusammen:
Untersuchen Sie die drei möglichen Fälle
,
und
.
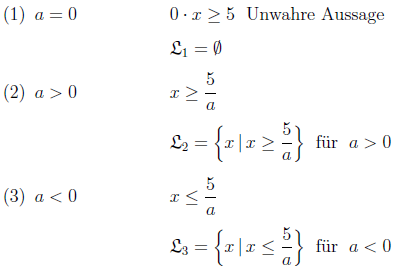
Fassen Sie nun die einzelnen Lösungsmengen der drei
Fälle zusammen.
b)
Verwenden Sie die binomischen Formeln, um
zusammenzufassen:
Nehmen Sie nun die Fallunterscheidungen für
,
und
vor.

Fassen Sie die Ergebnisse der Fallunterscheidungen
zusammen.
13.8 Quadratische Funktionen
Übung 8.3.1
Zeichnen Sie die folgenden Parabeln, indem
Sie schrittweise die Normalparabel verschieben, stauchen oder strecken.
| a) |
|
| b) |
|
| c) |
|
| d) |
. |
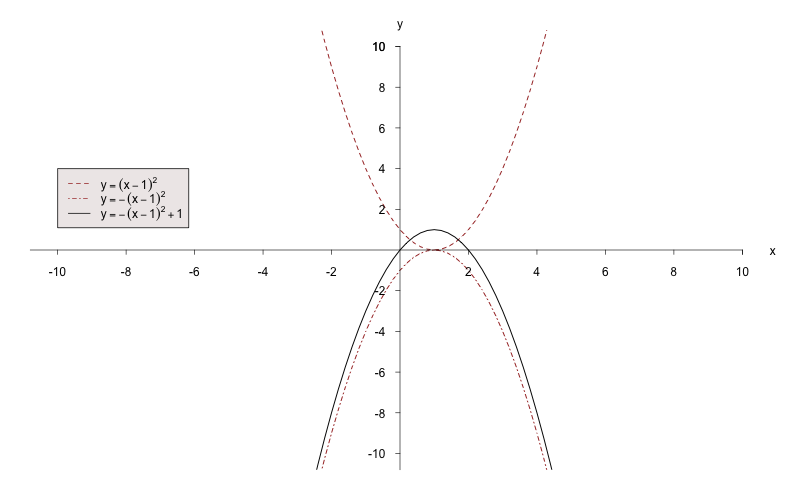
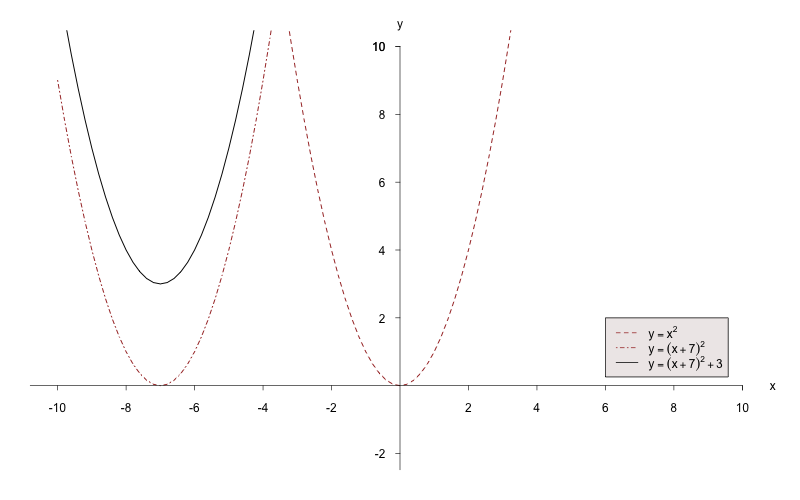
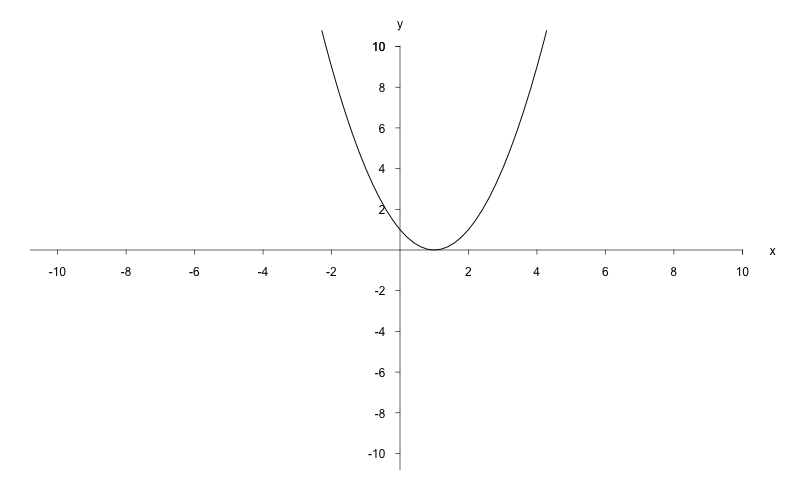
a)
Gehen Sie von einer Normalparabel aus und
zeichnen Sie zuerst
.
Dabei handelt es sich um eine nach rechts verschobene Parabel.
Zeichnen Sie nun
,
indem Sie die Funktion an der
-Achse
spiegeln.
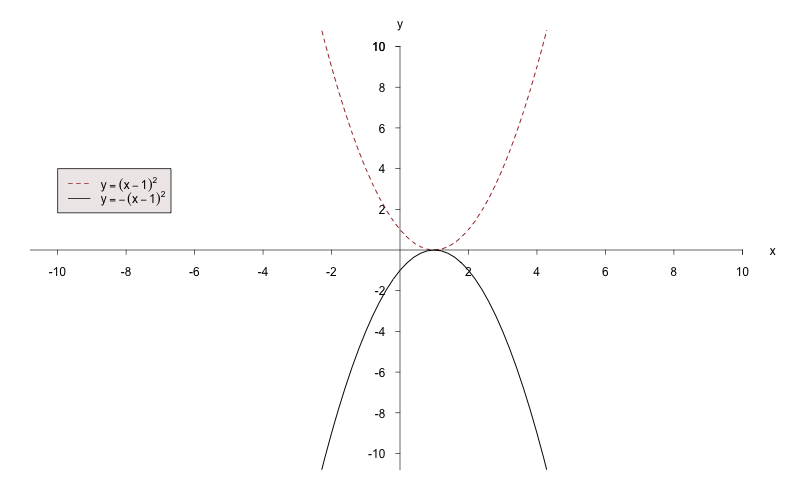
Nun wird die Funktion
um eine Einheit nach oben verschoben.
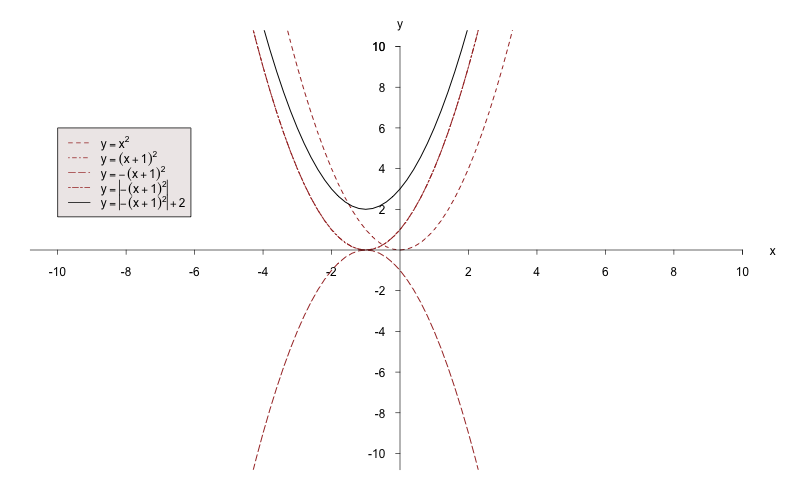
b)
Zeichnen Sie die Funktion
schrittweise:
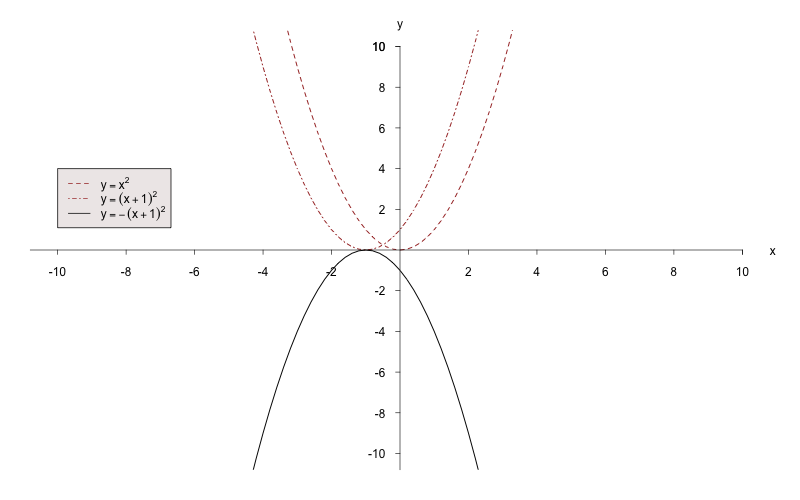
Spiegeln Sie den Bereich der Funktion, der unterhalb der
-Achse liegt, an der
-Achse.
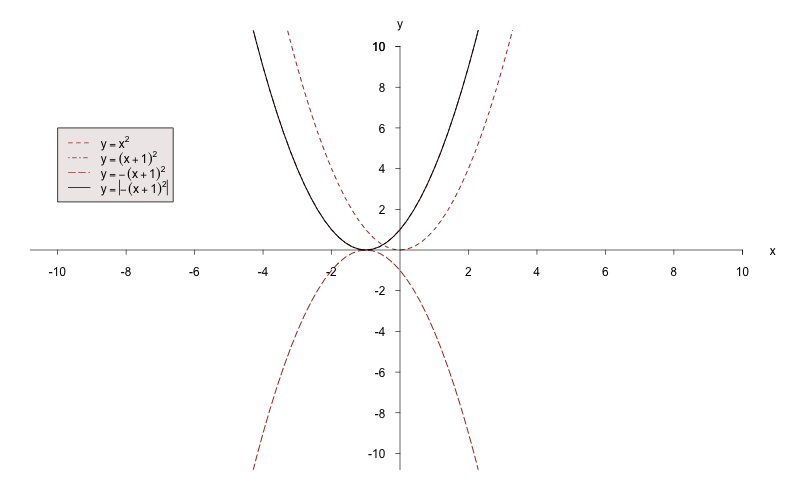
Nun muss die erhaltene Funktion noch um 2 Einheiten nach
oben verschoben werden.
c)
Um die Funktion exakt zeichnen zu können,
muss sie durch quadratische Ergänzung in die Scheitelpunktsform
gebracht werden.
In der Funktion steckt eine binomische Formel der Art .
Es muss nun ermittelt werden, wie groß
ist:
Nachdem
ermittelt wurde, kann das Wissen über binomische Formeln angewendet
werden:
Zeichnen Sie die Funktion, indem Sie die Normalparabel um 7
Einheiten nach links und um 3 Einheiten nach oben verschieben.
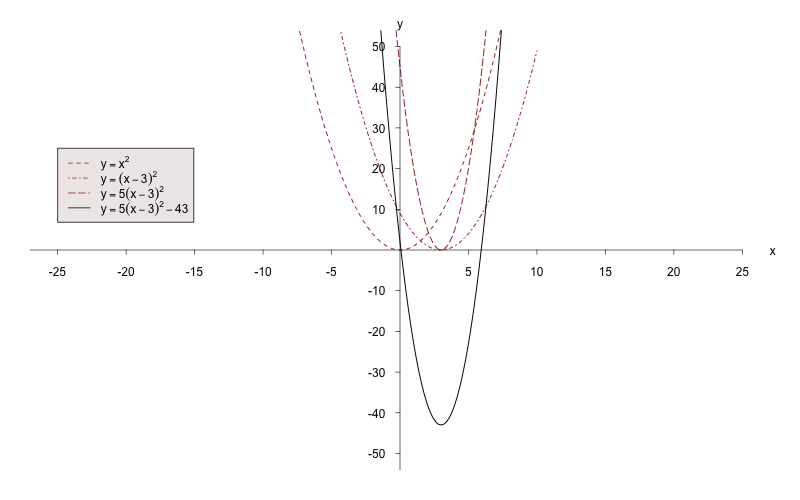
d)
Bringen Sie die Funktion durch quadratische
Ergänzung in die Scheitelpunktform. Klammern Sie dazu zunächst
5 aus:
Hinweis:
Wenn Sie 5 nicht ausklammern möchten, müssen
Sie berücksichtigen, dass die binomische Formel die Form
hat. Dies macht die Lösung komplizierter.
Ermitteln Sie nun in der Klammer die binomische Formel:
Zeichnen Sie nun die Funktion, indem Sie ihr Wissen
über Parameter bei Funktionen anwenden.
Übung 8.3.2
Berechnen Sie die Nullstellen folgender quadratischer Funktionen.
| a) |
|
| b) |
|
| c) |
für ,. |
a)
Die Nullstellen sind dadurch definiert, dass der -Wert Null ist. Deshalb muss die Funktion
Null gesetzt werden:
Formen Sie die Gleichung so um, dass die p-q-Formel
angewendet werden kann:
Wenden Sie nun die p-q-Formel
an.
Die Funktion hat nur eine Nullstelle bei
.
b)
Die Funktion ist auf ungewöhnliche Weise
dargestellt, doch es ist nicht notwendig das Produkt
auszumultiplizieren. Setzen Sie die Funktion stattdessen gleich Null:
Ein Produkt ist Null, wenn einer der Faktoren Null ist.
Deswegen reicht es aus, die Faktoren einzeln Null zu setzen.
Die Funktion hat zwei Nullstellen in den Punkten
und .
c)
Da
und
unbekannt sind, handelt es sich bei diesem
Beispiel um eine Funktionsschar. Gehen Sie dennoch wie gewohnt vor,
indem Sie die Funktion Null setzen:
Nun muss die Gleichung so umgeformt werden, dass die p-q-Formel
anwendbar ist:
Wenden Sie die p-q-Formel
an und vereinfachen Sie bereits in den Zwischenschritten so weit wie
möglich, um optimal zusammenfassen zu können.
Da wegen der quadratischen Ausdrücke gesichert ist,
dass der Ausdruck unter der Wurzel positiv ist, kann nun die Wurzel
gezogen werden.
Die Funktionsschar besitzt Nullstellen in den Punkten
und .
Übung 8.3.3
Gegeben sei die Parabel
Berechnen Sie die Schnittpunkte mit
| a) |
der Geraden |
|
| b) |
der Parabel |
|
| c) |
der Parabel |
|
a)
Setzen Sie beide Funktionen gleich, da ein
Schnittpunkt den gleichen -Wert in beiden
Funktionen annimmt.
Formen Sie die Gleichung um, so dass die -Formel
angewendet werden kann:
Mit Hilfe der -Formel
können die -Werte der Schnittpunkte
(also die Schnittstellen) ermittelt werden:
Nun müssen noch die -Werte
der Punkte ermittelt werden, indem man die -Werte
in eine der Funktionen einsetzt. Es bietet sich an, dazu die
Geradengleichung zu verwenden.
Die Funktionen schneiden sich näherungsweise in den Punkten
und .
b)
Setzen Sie die Funktionen gleich:
Formen Sie die Gleichungen um und wenden Sie die -Formel
an.
Es müssen noch die -Werte
der Schnittpunkte berechnet werden. Setzen Sie dazu die -Werte
in eine der Funktionen ein.
Die Parabeln schneiden sich näherungsweise in den Punkten
und .
c)
Gehen Sie trotz des Parameters
wie gewohnt vor, indem Sie die Funktionsvorschriften gleich setzen:
Formen Sie die Gleichung um und wenden Sie die
-Formel
an.
Achtung:
Es muss gesichert sein, dass der Term unter der Wurzel
positiv ist. Dies ist wegen des quadratischen Ausdrucks in diesem Fall
gesichert.
Nun müssen die -Werte
ermittelt werden.
Die Parabel schneidet die Parabelschar in den Punkten
und .
Übung 8.3.4
Berechnen Sie die Lösungsmenge folgender quadratischer
Ungleichungen
| a) |
|
|
indem Sie die Funktion nach der Nullstellenermittlung
zeichnen. |
|
|
| b) |
|
|
durch Einsetzen eines Probewertes nach Ermittlung der
Nullstellen. |
|
|
| c) |
|
|
durch ein selbstgewähltes Verfahren. |
a)
Stellen Sie die Ungleichung so um, dass die -Formel
anwendbar ist.
Wenden Sie die -Formel
nun an, um die Nullstellen der Funktion
zu ermitteln.
Nehmen Sie eine quadratische Ergänzung vor, um die
Funktion besser zeichnen zu können.
Zeichnen Sie die Funktion und notieren Sie die
Lösungsmenge.
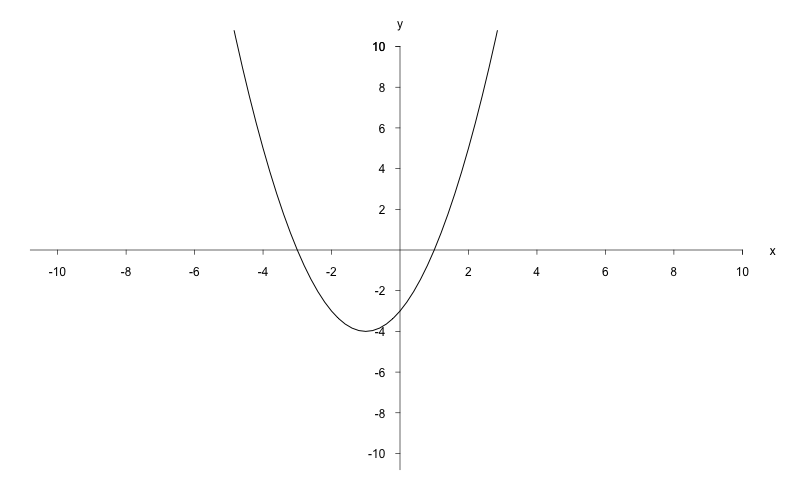
Hinweis:
Bitte beachten Sie, dass die Nullstellen nicht Teil der
Lösungsmenge sind.
b)
Beseitigen Sie zuerst die Brüche:
Stellen Sie die Ungleichung so um, dass Sie die Nullstellen
berechnen können.
Nun können die Nullstellen ermittelt werden.
Setzen Sie nun z.B. einen Wert zwischen
und
ein
um zu ermitteln, ob die Funktion
zwischen oder außerhalb der Nullstellen größer Null
ist. Wir wählen den Testwert 0:
Die Funktion ist also außerhalb der Nullstellen größer
Null.
bzw.
c)
Stellen Sie die Ungleichung um, sodass Sie leicht
die Nullstellen ermitteln können. Prüfen Sie genau, wie Sie
dies möglichst leicht erreichen können.
Hinweis:
Anstatt auszumultiplizieren kann leicht eine binomische
Formel angewendet werden. Dadurch kann während der Berechnung Zeit
gespart werden, was auch in Klausuren von großem Vorteil sein
kann. Sollten Sie mit den binomischen Formeln noch Probleme haben,
können Sie diese im entsprechenden Kapitel erneut üben.
Ermitteln Sie nun die Nullstellen.
Ermitteln Sie, ob die Funktion
zwischen oder außerhalb der Nullstellen negativ ist. Sie
können diese Untersuchung mit einem der beiden Verfahren aus den
Teilaufgaben a) und b) durchführen. Zum Beispiel können Sie
den Testwert 0 einsetzen:
Die Funktion ist also zwischen den Nullstellen negativ.
13.9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
Übung 9.3.1
Lösen Sie die Gleichung
Als erstes empfiehlt es sich, den Definitionsbereich zu
bestimmen. Dabei muss gelten
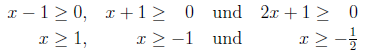
Somit lautet der Definitionsbereich
Nun sollte man die Gleichung auf beiden Seiten quadrieren.
Dabei ist besonders zu beachten, dass auf der linken Seite eine
binomische Formel entsteht.
Nun ist die Gleichung so umzuformen, dass auf einer Seite
die Wurzel steht und auf der anderen die restlichen Terme:
Tipp:
Nun lässt sich die Gleichung noch einmal auf beiden
Seiten quadrieren:
ausschließlich
da die andere denkbare Lösung
entfällt. Diese ist kein Teil des Definitionsbereiches.
Übung 9.3.2
Lösen Sie die Gleichung
Bestimmen Sie zunächst den Definitionsbereich für:
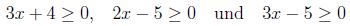
Damit lautet der Definitionsbereich
Anschließend sollten Sie die Gleichung wieder auf
beiden Seiten quadrieren. Wiederum ergibt sich auf der linken Seite eine
binomische Formel.
Nun können Sie die Gleichung so umformen, dass die
Wurzel auf einer Seite steht und der Rest auf der anderen:
Zur Vereinfachung wird die Gleichung durch −15 geteilt:
Jetzt können Sie die Gleichung noch einmal quadrieren
und die entstandene quadratische Gleichung lösen:
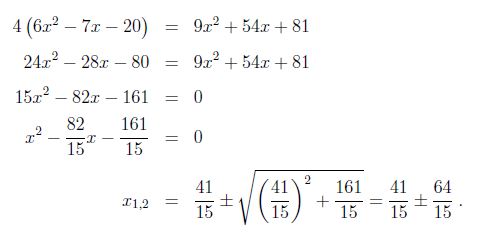
Die Lösung lautet:
Die Lösung
entfällt auf Grund der Unvereinbarkeit mit dem Definitionsbereich.
Übung 9.3.3
Lösen Sie die Gleichung
Bestimmen Sie zunächst wie gewohnt den
Definitionsbereich für
.
Damit gilt für den Definitionsbereich
Nun kann die Gleichung auf beiden Seiten quadriert werden.
Dabei ist auf die rechte Seite zu achten, da dort eine binomische Formel
auftritt.
Analog zu den vorherigen Übungen wird die Gleichung
nun so umgeformt, dass die Wurzel auf einer Seite der Gleichung isoliert
ist:
Anschließend wird der Ausdruck noch einmal quadriert
und die Formel nach
umgestellt:
Übung 9.3.4
Lösen Sie die Gleichung
|
. |
Bestimmen Sie zunächst den Definitionsbereich für :
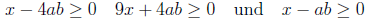
Der Definitionsbereich lautet somit
Die Gleichung wird nun auf beiden Seiten quadriert. Dabei
ist wiederum das Auftreten einer binomischen Formel auf der linken Seite
der Gleichung zu beachten.
In gewohnter Vorgehensweise wird die Wurzel auf einer Seite
der Gleichung isoliert:
Jetzt müssen Sie die Gleichung nur noch ein weiteres
Mal quadrieren und schließlich nach
auflösen.
13.10 Exponential- und Logarithmusfunktionen und -gleichungen
Übung 10.3.1
Lösen Sie die Gleichung
Wenden Sie die Potenzgesetze an und formen Sie die
Gleichung entsprechend um:
Vereinfachen Sie nun die Gleichung:
Bei gleicher Basis müssen die Exponenten gleich sein,
also muss gelten:
Übung 10.3.2
Lösen Sie die Gleichung:
Wenden Sie zunächst wieder die Potenzgesetze an:
Bei gleicher Basis müssen auch die Exponenten gleich
sein:
Nun muss die Gleichung nur noch nach
umgestellt werden.
Übung 10.3.3
Lösen Sie die Gleichung
Wenden Sie zunächst das entsprechende Potenzgesetz an
und formen Sie die Gleichung um:
Vereinfachen Sie anschließend den Term:
An dieser Stelle können Sie die Gleichung entweder
zur Basis 2 logarithmieren oder weiter vereinfachen. (
und )
Übung 10.3.4
Lösen Sie die Gleichung
Da die Basis auf beiden Seiten der Gleichung verschieden
ist, sollten Sie zuerst zur Basis 2 logarithmieren:
Die Gleichung sollten Sie nun so umformen, dass die
Ausdrücke aus dem Nenner verschwinden:
Nun können sie die Gleichung leicht umformen und zu einer quadratischen Gleichung vereinfachen:
Die enstandene Gleichung können Sie nun in gewohnter Weise lösen. Abschließend sollten Sie die Probe nicht vergessen
Die Lösung lautet
Nun können Sie die Gleichung leicht umformen und vereinfachen:
Die entstandene quadratische Gleichung können Sie nun in gewohnter
Weise lösen. Abschließend sollten Sie die Probe nicht
vergessen.
Übung 10.3.5
Lösen Sie die Gleichung
Der Defionitionsbereich der Gleichung ist .
Stellen Sie die Gleichung so um, dass alle logarithmischen
Ausdrücke auf einer Seite stehen:
Wenden Sie nun das betreffende Logarithmengesetz an, um die
beiden Ausdrücke zusammenzufassen:
Da es sich um einen dekadischen Logarithmus handelt, folgt
Nun müssen Sie die Gleichung nur noch nach
auflösen.
Dieser Wert liegt im Definitionsbereich und erfüllt die Ausgangsgleichung.
Übung 10.3.6
Lösen Sie die Gleichung
Fassen Sie zunächst die beiden
Logarithmus-Ausdrücke zusammen:
Lösen Sie nun den Logarithmus auf:
Nun können Sie die Gleichung auf beiden Seiten
quadrieren.
Übung 10.3.7
Lösen Sie folgende Gleichung nach
auf:
Der Definitionsbereich der Gleichung ist .
Formen Sie die Gleichung zuerst mit den passenden
Logarithmengesetzen um und versuchen Sie dabei eine Vereinfachung
herbeizuführen:
Lösen Sie nun den Logarithmus auf:
Die somit entstandene Gleichung lässt sich nun leicht
mit Hilfe der --Formel
auflösen.
und
gehört zum Definitionsbereich und erfüllt die Ausgangsgleichung. liegt nicht im Definitionsbereich und ist eine Scheinlösung.
Übung 10.3.8
Lösen Sie die Gleichung nach
auf:
Formen Sie die Gleichung zunächst um:
In dieser Situation bietet sich eine Substitution der Form
an:
Stellen Sie die Gleichung nun so um, dass der
Wurzelausdruck auf einer Seite isoliert ist:
Nun können Sie die Gleichung quadrieren und erhalten
Schließlich müssen Sie die Ausdrücke
resubstituieren und erhalten
13.11 Trigonometrische Funktionen
Übung 11.3.1
Lösen Sie folgende Gleichung:
Ersetzen Sie zunächst
durch :
Klammern Sie nun
aus:
Bei einem Produkt, das gleich
ist, muss einer der Faktoren ebenfalls
sein:
Nun können Sie beide Gleichungen separat lösen:
Übung 11.3.2
Lösen Sie die Gleichung
|
. |
Wenden Sie den trigonometrischen Satz des Pythagoras an: .
Nun können Sie die Gleichung vereinfachen und
substituieren:
Lösen Sie anschließend die quadratische
Gleichung und resubstituieren Sie die trigonometrische Funktion.
Der Ausdruck
ist nicht lösbar, da der Wertebereich der Sinusfunktion
ist.
Übung 11.3.3
Vereinfachen Sie den folgenden
Ausdruck:
Nutzen Sie die Formel
.
Für
gilt dann:
Es folgt für die Ausgangsgleichung somit
Wenden Sie nun die erste binomische Formel an:
Jetzt können Sie den trigonometrischen Pythagoras
nutzen:
Übung 11.3.4
Vereinfachen Sie folgenden Ausdruck:
Mit Hilfe des trigonometrischen Satzes des Pythagoras
erhalten Sie
Nun können Sie die zweite binomische Formel anwenden:
Nun wenden Sie nochmals den trigonometrischen Satz des
Pythagoras an:
Nun können Sie noch
ausklammern und das Additionstheorem für
anwenden:
13.12 Funktionen in Polarkoordinaten
Übung 12.3.1
| a) |
Welche Polarkoordinaten besitzen die Punkte ,? |
| b) |
Wie lauten die kartesischen Koordinaten der Punkte , |
a)
Nutzen Sie die gegebenen Formeln für die
Umrechnung und setzen Sie die Werte ein:
Der Winkel
liegt im 1. Quadranten, der Winkel
befindet sich im 4. Quadranten.

b)
Die Werte für
und
müssen nur in die
entsprechenden Formeln eingesetzt werden:
Die Lösung ist demnach
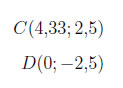
Übung 12.3.2
Wie lautet die folgende Kurvengleichung in
Polarkoordinaten?
Zur Umrechnung einer Kurvengleichung werden die folgenden
Formeln verwendet:
Diese können Sie in die gegebene Kurvengleichung einsetzen:
Klammern Sie nun
aus beiden
Ausdrücken aus:
Beachten Sie, dass
und
ist, dann erhalten Sie folgende Vereinfachung:
Teilen Sie die ganze Gleichung durch
und stellen Sie diese dann nach
um.
Übung 12.3.3
Wie lautet die folgende Kurvengleichung in
kartesischen Koordination?
Die Formeln
können Sie nach
und
umstellen.
Beachtet man noch, dass
ist, dann erhalten Sie
Nun können Sie diese Ausdrücke in die ursprüngliche
Formel einsetzen:
Nun können Sie die beiden Terme im Nenner
zusammenfassen:
Nun können Sie die Gleichung auf beiden Seiten mit
multiplizieren. Anschließend können Sie die Gleichung durch
teilen und alles auf eine Seite der Gleichung bringen.
Übung 12.3.4
Wie lautet die Kurvengleichung in
kartesischen Koordinaten?
Es gilt:
Aus den Formeln ,
und
können Sie
und
herleiten.
Diesen Schritt haben Sie bereits in Übung 12.3.3 geübt. Nun setzen Sie
die Ausdrücke in die gegebene Gleichung ein:
Die Gleichung können Sie jetzt mit
multiplizieren und anschließend alle Terme auf eine Seite bringen.