6 Funktionen

6.1 Theorie

Eine Funktion ordnet jedem Wert $x$ aus einer Menge durch eine Vorschrift $f$ eindeutig einen Wert $y$ aus einer weiteren Menge zu: $y$ ist eine von $x$ abhängige Variable. Notiert wird eine Funktion durch $y = f (x)$ .
Die Menge aller Variablen 𝑥, für die die Funktion erklärt ist, nennt man Definitionsmenge $D_{f} = D (f)$ . Alle zugeordneten 𝑦-Werte (Bilder) gehören zum Wertebereich $W_{f} = W (f)$ . Funktionen besitzen oft die elementaren Eigenschaften Monotonie, Symmetrie und Periodizität, die nachfolgend erläutert werden.

Eigenschaften von Funktionen

Monotonie

Mit Hilfe des Monotoniebegriffes lässt sich der Verlauf einer Funktion näher beschreiben. Es existieren 4 Monotoniearten:

Eine Funktion heißt streng monoton wachsend, wenn der nachfolgende Funktionswert stets größer ist als der vorherige.
$Für x_{1}, x_{2} \in D_{f}, x_{1} < x_{2} gilt f (x_{1}) < f (x_{2}) .$
Beispielhaft dargestellt ist die streng monoton wachsende Funktion $y = f (x) = x$ :
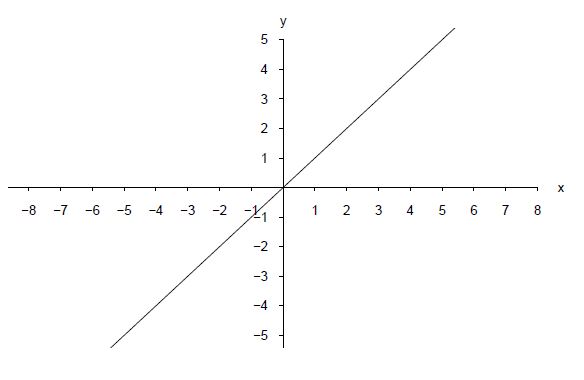
Eine Funktion heißt monoton wachsend, wenn auch die Gleichheit der Funktionswerte zugelassen wird.
$Für x_{1} < x_{2} gilt f (x_{1}) \leq f (x_{2}) .$
Die Abbildung zeigt eine monoton wachsende Funktion:
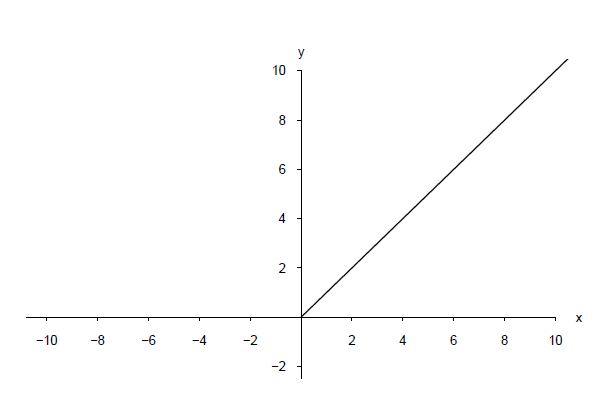
Eine Funktion kann auch streng monoton fallend sein.
$Für x_{1} < x_{2} gilt f (x_{1}) > f (x_{2}) .$
Das Beispiel zeigt die streng monoton fallende Funktion $y = f (x) = - x$ :
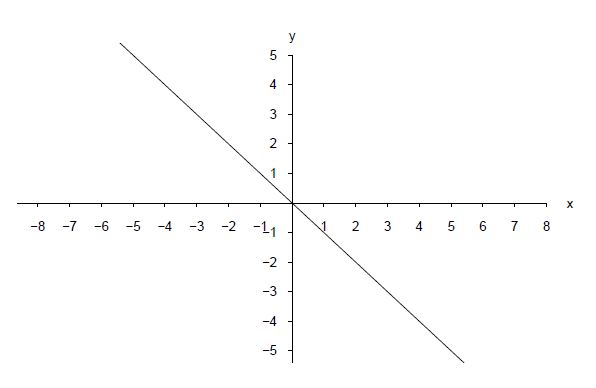
Analog heißt eine Funktion monoton fallend, wenn auch eine Gleichheit der Funktionswerte zugelassen ist.
$Für x_{1} < x_{2} gilt f (x_{1}) \geq f (x_{2}) .$
Diese Abbildung zeigt eine monoton fallende Funktion:

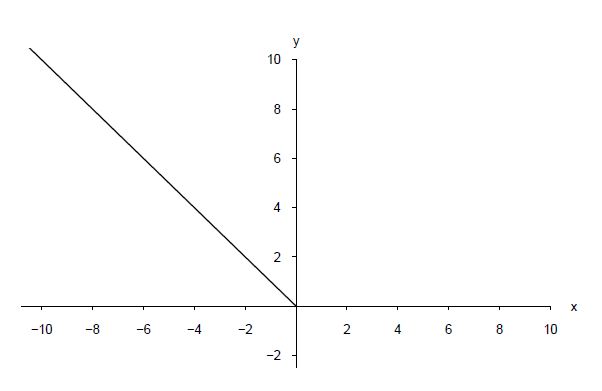
Hinweis: Die dargestellten Beispiele sind für den gesamten Definitionsbereich monoton. Die Monotonie einer Funktion kann auch auf Intervallen beschrieben werden, wenn eine Funktion auf dem gesamten Definitionsbereich nicht einer Monotonieart zugeordnet werden kann.

Symmetrie

Der Graph einer Funktion kann symmetrisch zu einer Geraden oder symmetrisch zu einem Punkt verlaufen. Man unterscheidet folgende Symmetriearten:

Achsensymmetrie: Eine Funktion ist achsensymmetrisch zur $y$ -Achse, wenn gilt:
$Für
alle x \in D_{f} gilt f (x) = f (- x) .$
Die unten abgebildete Funktion ist achsensymmetrisch, da gilt
$f (- x) = {(- x)}^{2} = x^{2} = f (x)$

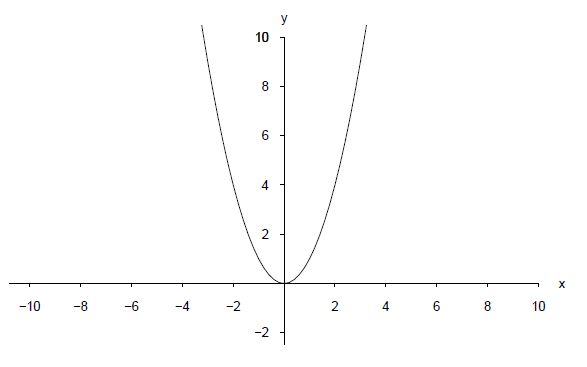
Hinweis: Es existieren auch noch Achsensymmetrien bezüglich anderer Achsen, jedoch soll auf diese hier nicht weiter eingegangen werden.
Punktsymmetrie: Eine Funktion wird als punktsymmetrisch zum Ursprung bezeichnet, wenn gilt:
$Für
alle x \in D_{f} gilt - f (x) = f (- x) .$
Die Grafik zeigt eine punktsymmetrische Funktion, für die die Bedingung erfüllt ist:
$f (- x) = {(- x)}^{3} = - x^{3} = - f (x)$

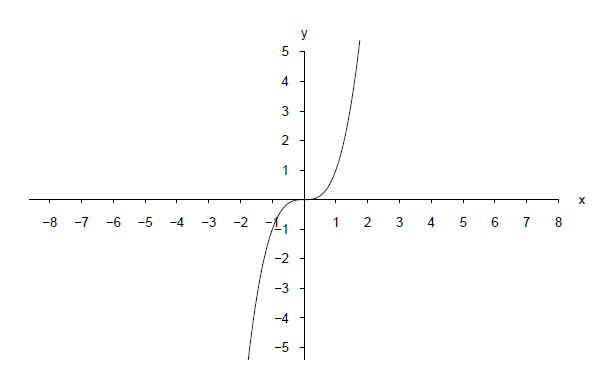
Hinweis: Wiederum existieren auch noch Punktsymmetrien bezüglich anderer Punkte, jedoch soll auf diese hier nicht weiter eingegangen werden.

Periodizität

Eine Funktion heißt periodisch, wenn sich die Funktionswerte in regelmäßigen Abständen wiederholen. Mathematisch wird dies durch folgende Formel ausgedrückt:

f (x) = f (x + k T)

k = 0, \pm 1, \pm 2, \dots

$T$ bezeichnet man als Periode. Wichtige periodische Funktionen sind die trigonometrischen Funktionen, von denen z.B. Sinus und Cosinus eine kleinste Periode von $2 π$ besitzen.

Umkehrbarkeit

Funktionen sind umkehrbar, wenn sie für den gesamten Definitionsbereich streng monoton wachsen oder streng monoton fallend sind. Sollte dieses Kriterium nur für Intervalle des Definitionsbereichs erfüllt sein, so ist die Funktion nur für diese Intervalle umkehrbar. Es existiert eine Umkehrfunktion

y = f^{- 1} (x)

. Dies darf nicht mit

y = \frac{1}{f (x)}

verwechselt werden. Der Definitionsbereich der Funktion entspricht dem Wertebereich der Umkehrfunktion und der Wertebereich der Funktion entspricht dem Definitionsbereich der Umkehrfunktion.

Wenn das Kriterium überprüft wurde, kann die Umkehrfunktion gezeichnet werden, indem man die Funktion an der Winkelhalbierenden $y = x$ spiegelt. Dabei sollte beachtet werden, dass jede Umkehrfunktion pro Intervall mit strenger Monotonie, eine eigenständige Funktion ist.

Die Umkehrfunktion kann berechnet werden, indem man

Die Funktion umstellt, bis die Variable $x$ allein auf einer Seite steht.
Anschließend die Variablen formal vertauscht, sodass $y$ durch $x$ ersetzt wird und $x$ durch $y$ .

Auch bei der Berechnung der Umkehrfunktion sind die möglichen Intervalle, auf denen die Umkehrfunktionen existieren, zu berücksichtigen. Dies werden wir z.B. in den Kapiteln 9, 10 und 11 üben.

Entsprechendes Videomaterial finden Sie hier.

Wirkung von Parametern

In der Technik ist es von Bedeutung zu wissen, wie sich die Parameter $a$ , $b$ , $c$ und $d$ auf Funktionen der Art $y = a \cdot f (b x + c) + d$ auswirken.

Verschieben durch $c$ und $d, c > 0, d > 0$

$y = f (x) + d$	Der Graph der Funktion wird um $d$ nach oben verschoben.
$y = f (x) - d$	Der Graph der Funktion wird um $d$ nach unten verschoben.
$y = f (x - c)$	Der Graph der Funktion wird um $c$ nach rechts verschoben.
$y = f (x + c)$	Der Graph der Funktion wird um $c$ nach links verschoben.

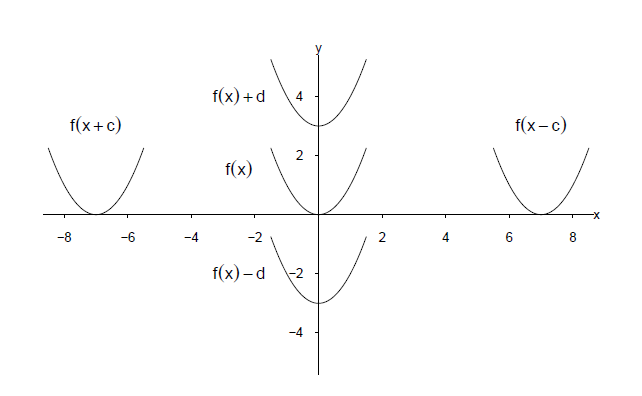
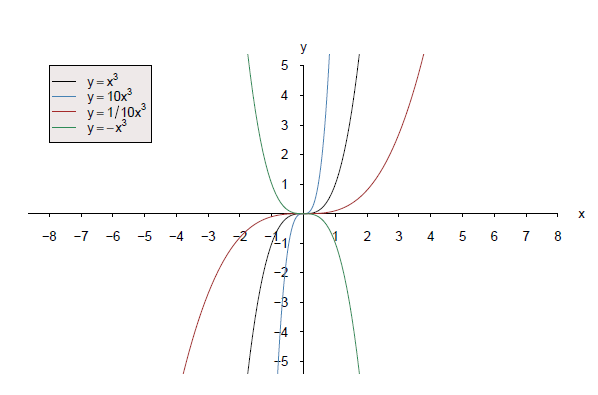
Stauchen, Strecken und Spiegeln durch $a$ und $b$

$\| a \| > 1$	Streckung in $y$ -Richtung.
$\| a \| < 1$	Stauchung in $y$ -Richtung.
$a < 0$	Spiegelung an der $x$ -Achse.
$\| b \| > 1$	Stauchung in $x$ -Richtung.
$\| b \| < 1$	Streckung in $y$ -Richtung.
$b < 0$	Spiegelung an der $y$ -Achse.

Hinweis: Wenn $b \neq 1$ , dann wird in der Funktion $y = f (b \cdot x + c)$ der um $b$ gestreckte bzw. gestauchte Funktionsgraph nur um $(c / b)$ verschoben.

Die folgenden Videos sollen die theoretischen Erläuterungen unterstützen:

Funktionsbegriff	Grundlegende Eigenschaften von Funktionen

Funktionen Übung 1	Umkehrfunktion

Diese Videos sind Bestandteil des Moodle-Projekts innerhalb der HTW Berlin.