10 Exponential- und Logarithmusfunktionen und -gleichungen

Zum Test

10.1 Theorie

10.1.1 Exponentialfunktionen

Eine Funktion der Form

$f\left(x\right)=a^{\mathrm{x}} \mathrm{mit} a{\mathrm{ ϵ ℝ}}^{+}$

heißt Exponentialfunktion zur Basis $a$.

Grundlegende Eigenschaften sind:

• Der Definitionsbereich der Exponentialfunktion ist $ℝ$.
• Für $a>1$ ist die Funktion monoton steigend, für $0<a<1$ ist die Funktion streng monoton fallend. Alle Graphen enthalten den Punkt $(0;1)$, denn es gilt $a^0=1$ für alle $xϵ{ℝ}^{\mathrm{+}}$.

• Beispiel:

  

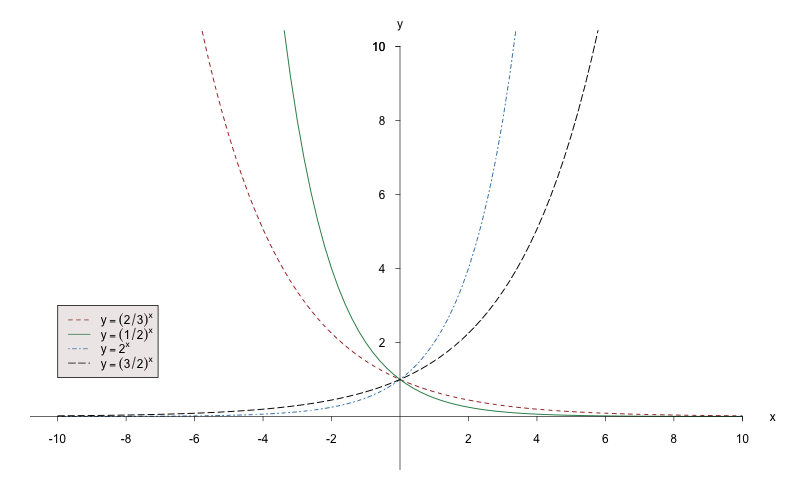
Ein Spezialfall der Exponentialfunktion ist die $e$-Funktion

${\displaystyle f\left(x\right)=e^x.}$

In der Literatur wird die $e$-Funktion auch oft dargestellt durch

${\displaystyle f\left(x\right)=e^x=\exp \left(x\right).}$

Die Zahl $e$ heißt Eulerzahl mit $e=2,718281828\dots$ und hat in der Mathematik eine große Bedeutung. Das Besondere an der $e$-Funktion ist, dass das Verhältnis aus der Kurvensteigung und dem Funktionswert an jeder Stelle konstant gleich $1$ ist.

10.1.2 Logarithmusfunktionen

Eine Funktion der Form

${\displaystyle f\left(x\right)={\log }_{a}x}$

heißt Logarithmusfunktion. Sie ist für die Exponentialfunktion $f\left(x\right)=a^x$ die Umkehrfunktion.

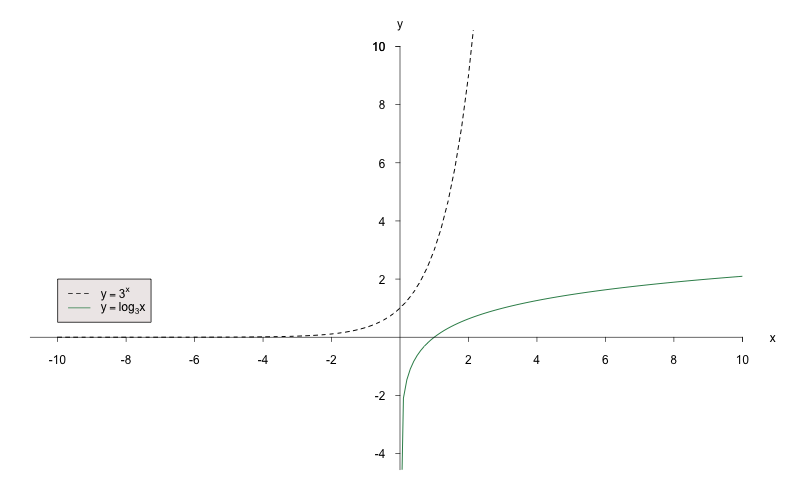
Grundlegende Eigenschaften sind:

• Der Definitionsbereich der Logarithmusfunktion ist ${ℝ}^{+}$.

• Auf Grund von

  ${\displaystyle a^0=1\iff {\log }_{a}1=0}$

  haben alle Graphen der Logarithmusfunktion den gemeinsamen Punkt$(0;1)$.

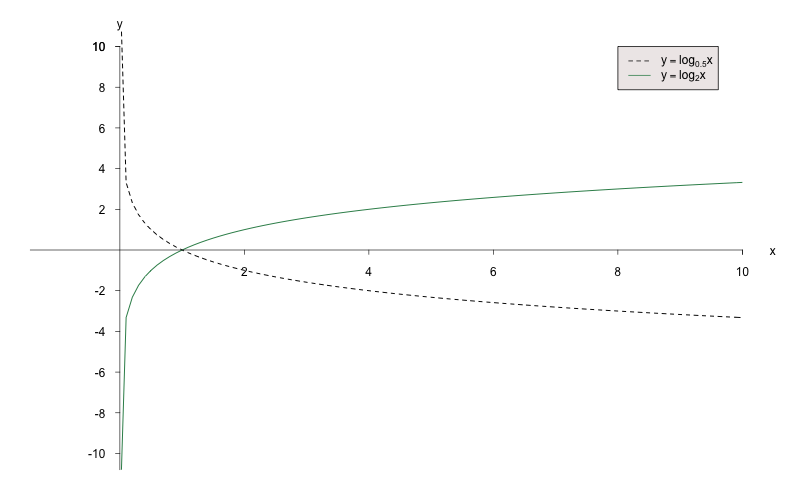
• Für $a>1$ ist die Funktion streng monoton steigend.
• Für $0<a<1$ ist die Funktion streng monoton fallend.

• Beispiel:

  

Was bedeutet log?

Die Gleichung $a^x=b$ ist lösbar und die Lösung lautet $x={\log }_{a}b$ mit $a,b\in {ℝ}^{+}$ und $x\in ℝ$.

Definition: Der Logarithmus von einer positiven reellen Zahl $b$ zur Basis $a$ ist diejenige Zahl $x$, mit der man $a$ potenzieren muss, um $b$ zu erhalten.

Zum Beispiel:

${\displaystyle 2^x=8\iff {\log }_{2}8=x\iff x=3}$

Spezialfälle des Logarithmus:

${\log }_{10}b$	$=$	$\lg b$	wird als dekadischer Logarithmus bezeichnet ($a$ = 10).
${\log }_{e}b$	$=$	$\ln b$	wird als natürlicher Logarithmus bezeichnet ($a$ = $e$).
${\log }_{2}b$	$=$	$\mathrm{lb} b$	wird als binärer Logarithmus bezeichnet ($a$ = 2).

Logarithmengesetze (Die Basis $a$ wird oft nicht angegeben):

 

$\log (x\cdot y)=\log \left(x\right)+\log \left(y\right)$		$\log \left(\frac{x}{y}\right)=\log \left(x\right)-\log \left(y\right)$
$\log \left(x^y\right)=y\cdot \log \left(x\right)$		$\log \left(\sqrt[y]{x}\right)=\frac{1}{y}\cdot \log \left(x\right)$
${\log }_{a}1=0$		${\log }_{a}a=1$
${\log }_x\mathrm{b}=\frac{{\log }_{a}b}{{\log }_{a}x}$

10.1.3 Exponentialgleichungen

Exponentialgleichungen sind Gleichungen, bei denen die Variable ausschließlich im Exponenten auftritt. Solche Gleichungen lassen sich durch Gleichsetzen der Exponenten (bei gleicher Basis) oder durch Logarithmieren (bei unterschiedlicher Basis) lösen. Dabei sind die Potenz- und Logarithmengesetze zu beachten. Die praktische Lösung dieser Art von Gleichungen wird ausführlich an den nachfolgenden Beispielen erläutert.

10.1.4 Logarithmusgleichungen

Beim Lösen von Logarithmusgleichungen ist zu beachten, dass der Definitionsbereich der Gleichung stark eingeschränkt sein kann. Deswegen ist es wichtig, jede Lösung mit einer abschließenden Proberechnung zu überprüfen.

Allgemein lassen sich logarithmische Gleichungen durch geeignete Umformungen (insbesondere durch die Anwendung der Logarithmengesetze) lösen. Nachfolgende Beispiele erläutern den genauen Lösungsweg.

Die folgenden Videos sollen die theoretischen Erläuterungen unterstützen:

Exponential- und Logarithmusfunktionen	Exponentialgleichungen 1	Exponentialgleichungen 2
Exponentialgleichungen 3	Exponentialgleichungen 4	Rechnen mit Logarithmen 1
Rechnen mit Logarithmen 2	Rechnen mit Logarithmen 3	Logarithmische Gleichungen 1
Logarithmische Gleichungen 2            Logarithmische Gleichungen 3
Diese Videos sind Bestandteil des Moodle-Projekts innerhalb der HTW Berlin.

10.2 Beispiele

Beispiel 10.2.1

Lösen Sie die Gleichung

${\displaystyle 6^{3x+9}={36}^{2x+5}.}$

Lösung: Zunächst sehen die beiden Basen unterschiedlich aus. Betrachtet man diese aber genauer, so fällt auf, dass man $36$ zerlegen kann zu

${\displaystyle 36=6\cdot 6=6^2.}$

Anschließend kann man wie folgt umformen:

${\displaystyle 6^{3x+9}={\left(6^2\right)}^{2x+5}.}$

Jetzt kann man das Potenzgesetz ${\left(a^n\right)}^m=a^{nm}$ anwenden:

${\displaystyle 6^{3x+9}=6^{2(2x+5)}.}$

Wenn zwei Potenzen mit gleicher Basis gleich sein sollen, dann müssen auch die Exponenten übereinstimmen:

${\displaystyle \begin{array}{rcl}3x+9& =& 2(2x+5)\\ 3x+9& =& 4x+10\\ -x& =& 1\\ x& =& -1.\end{array}}$

Schließlich kann noch eine Probe durchgeführt werden:

${\displaystyle \begin{array}{rcl}{6}^{3\cdot (-1)+9}& =& {36}^{2\cdot (-1)+5}\\ 6^6& =& {36}^3\\ 46656& =& 46656.\end{array}}$

Beispiel 10.2.2

Lösen Sie die Gleichung

${\displaystyle 5^x-5^{x-1}=100.}$

Lösung: Diese Gleichung kann man nicht mit der gleichen Methode wie im Beispiel 1 lösen, da hier neben den Potenzen noch ein Term ohne Exponenten auftritt. Daher sollte man als erstes versuchen, die Gleichung soweit möglich zu vereinfachen:

${\displaystyle 5^x-5^x\cdot 5^{-1}=100}$

Nun kann man $5^x$ ausklammern:

${\displaystyle \begin{array}{rcl}{5}^x(1-\frac{1}{5})& =& 100\\ 5^x\cdot 0,8& =& 100\\ 5^x& =& 125.\\ 5^x& =& 5^3\\ x& =& 3\end{array}}$

Alternativ hätten Sie die Gleichung ${\displaystyle \begin{array}{rcl}{5}^x& =& 125\end{array}}$ auf beiden Seiten logarithmieren können um dann nach x aufzulösen:

${\displaystyle \begin{array}{rcl}x\cdot \lg 5& =& \lg 125\\ x& =& \frac{\lg 125}{\lg 5}\\ x& =& 3.\end{array}}$

Anschließend sollten Sie noch eine Probe durchführen:

${\displaystyle \begin{array}{rcl}{5}^3-5^{3-1}& =& 100\\ 100& =& 100.\end{array}}$

Beispiel 10.2.3

Lösen Sie folgende Gleichung:

${\displaystyle {\log }_{x}9=1+{\log }_{x}3.}$

Lösung: Als erstes sollten Sie die Gleichung umformen, um sie auf die Form ${\log }_{x}b=a$ zu bringen:

${\displaystyle {\log }_{\mathrm{x}}9-{\log }_{x}3=1.}$

Nun kann man die Logarithmengesetze anwenden:

${\displaystyle \begin{array}{rcl}{\log }_x\left(\frac{9}{3}\right)& =& 1\\ {\log }_{x}3& =& 1.\end{array}}$

Nun kann die Gleichung in eine Potenz umgeformt werden:

${\displaystyle \begin{array}{rcl}3& =& x^1\\ x& =& 3.\end{array}}$

Nun sollten Sie noch eine Probe durchführen:

${\displaystyle \begin{array}{rcl}{\log }_{3}9& =& 1+{\log }_{3}3\\ 2& =& 2.\end{array}}$

Beispiel 10.2.4

Lösen Sie die Gleichung

${\displaystyle \ln (x^2+4x+2)-\ln (x+12)=0.}$

Lösung: Zunächst wird der Definitionsbereich der Gleichung bestimmt:

${\mathrm{x}}^2+4 x+2>0 \mathrm{gilt} \mathrm{für} xϵ \left(-\infty ,-2-\sqrt{2}\right)\cup \left(-2 +\sqrt{2},\infty \right)$ $x+12>0 \mathrm{ist} \mathrm{für} x>-12 \mathrm{erfüllt}. \mathrm{Für} \mathrm{den} \mathrm{Definitionsbereich} \mathrm{erhält} \mathrm{man} \mathrm{somit}$ $𝔻=\left(-12,-2,-2\sqrt{2}\right)\cup \left(-2+\sqrt{2},\infty \right) .$

Zur Berechnung der Lösungsmenge formen Sie die Gleichung zunächst um:

${\displaystyle \ln (x^2+4x+2)=\ln (x+12).}$

Nun können Sie die Regel ${\log }_a{T}_1\left(x\right)={\log }_a{T}_2\left(x\right)\iff T_1\left(x\right)=T_2\left(x\right)$ anwenden, wobei $T_1\left(x\right)$ und $T_2\left(x\right)$ Funktionen sind.

${\displaystyle x^2+4x+2=x+12}$

Nun ist die Gleichung einfach zu lösen durch Umformung und Anwendung der $p$-$q$-Formel:

${\displaystyle x^2+3x-10=0}$ ${\displaystyle \begin{array}{rcl}{x}_{1,2}& =& -1,5\pm \sqrt{2,25+10}\\ x_1=-5& & x_2=2\end{array}}$

Beide Werte liegen im Deffionitionsbereich.

Abschließend ist noch die Proberechnung durchzuführen:

$\mathrm{x=-5}$				$\mathrm{x=+2}$
$\ln (25-20+2)-\ln (-5+12)$	$=$	$0$		$\ln (4+8+2)-\ln (2+12)$	$=$	$0$
$\ln 7-\ln 7$	$=$	$0$		$\ln 14-\ln 14$	$=$	$0$
$0$	$=$	$0$		$0$	$=$	$0$

Die Lösungsmenge ist demnach

${\displaystyle L=\{-5;2\}.}$

Der folgende Pencast erläutert ausführlich eine weitere Beispielaufgabe:

10.3 Übungen

Die Lösungen zu den hier gestellten Übungen finden Sie im Kapitel "Hinweise und Lösungen zu den Übungen". Zu jeder Übung wird eine Bearbeitungszeit vorgegeben.

Übung 10.3.1

Lösen Sie die Gleichung

${\displaystyle 2^{2x+3}+3\cdot 2^{2x}=22.}$ Bearbeitungszeit: 8 Minuten

Übung 10.3.2

Lösen Sie die Gleichung:

${\displaystyle \sqrt{a^{3x-7}}=\sqrt[3]{a^{4x-3}}.}$ Bearbeitungszeit: 10 Minuten

Übung 10.3.3

Lösen Sie die Gleichung

${\displaystyle 4^{x+3}-13\cdot 4^{x+1}=2^{3x-1}-2^{3x-3}.}$ Bearbeitungszeit: 10 Minuten

Übung 10.3.4

Lösen Sie die Gleichung

${\displaystyle {32}^{\frac{2x+1}{x+2}}=4^{\frac{6x-1}{4x-1}}.}$ Bearbeitungszeit: 12 Minuten

Übung 10.3.5

Lösen Sie die Gleichung

${\displaystyle \lg (2x+3)=\lg (x+1)+1.}$ Bearbeitungszeit: 10 Minuten

Übung 10.3.6

Lösen Sie die Gleichung

${\displaystyle {\log }_x\sqrt{2}+{\log }_{x}4=\frac{1}{2}.}$ Bearbeitungszeit: 12 Minuten

Übung 10.3.7

Lösen Sie folgende Gleichung nach $x$ auf:

${\displaystyle \frac{1}{2}\lg (2x-1)+\lg \sqrt{x-9}=1.}$ Bearbeitungszeit: 12 Minuten

Übung 10.3.8

Lösen Sie die Gleichung nach $x$ auf:

${\displaystyle 3\cdot \sqrt{\lg \left(x\right)}-\lg \left(x\right)=2.}$ Bearbeitungszeit: 12 Minuten


Zum Test

• Startseite
• Einführung
• Inhaltsverzeichnis
  • 1 Umstellen von Gleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 2 Potenzen und Wurzeln
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 4 Polynomdivision
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 5 Mengenlehre
    • Theorie
  • 6 Funktionen
    • Theorie
  • 7 Lineare Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 8 Quadratische Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 11 Trigonometrische Funktionen
    • Theorie
    • Beispiele
    • Übungen
    • Test
  • 12 Funktionen in Polarkoordinaten
    • Theorie
    • Beispiele
    • Übungen
    • Test
• 13 Hinweise und Lösungen zu den Übungen
  • 1 Umstellen von Gleichungen
  • 2 Potenzen und Wurzeln
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
  • 4 Polynomdivision
  • 7 Lineare Funktionen
  • 8 Quadratische Funktionen
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
  • 11 Trigonometrische Funktionen
  • 12 Funktionen in Polarkoordinaten
• 14 Hinweise und Lösungen zu den Tests
  • 1 Umstellen von Gleichungen
  • 2 Potenzen und Wurzeln
  • 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
  • 4 Polynomdivision
  • 7 Lineare Funktionen
  • 8 Quadratische Funktionen
  • 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
  • 10 Exponential- und Logarithmusfunktionen und -gleichungen
  • 11 Trigonometrische Funktionen
  • 12 Funktionen in Polarkoordinaten