für Studienanfänger technischer Studiengänge
3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
Zum Test3.1 Theorie
Mit Hilfe des Binomialkoeffizienten kann bestimmt werden, auf wie viel verschiedene Arten Elemente aus einer -elementigen Menge ausgewählt werden können. Dabei ist die Reihenfolge unerheblich und die Elemente dürfen nicht zurückgelegt werden.
Der Binomialkoeffizient wird folgender Maßen berechnet:
Der Ausdruck für den Binomialkoeffizienten wird “n
über k” gesprochen. Das Symbol "!"
wird Fakultät genannt.
Zum Beispiel steht "5!" für
.
Weiterhin gilt:
Ein bekannte Anwendung wäre zum Beispiel die Ziehung der Lottozahlen ohne Zusatzzahlen, denn es werden 6 Zahlen aus 49 gezogen. Es gibt also entsprechend viele Möglichkeiten:
Tipp: Sollten die Fakultäten zu groß für die Taschenrechnerkapazität sein, so kann man wie im Beispiel Faktoren, die im Nenner und Zähler vorkommen, kürzen.
Der Name Binomialkoeffizient stammt von der Verwendung des Terms als Koeffizienten im binomischen Lehrsatz. Dieser dient zur Berechnung von potenzierten Summen zweier Variablen, bekannt sind vor allem die so genannten binomischen Formeln.
Der binomische Lehrsatz ist definiert durch:
Die benötigten Binomialkoeffizienten können berechnet oder aus dem Pascalschen Dreieck abgelesen werden:
| 1 | ||||||||||||||
| 1 | 1 | |||||||||||||
| 1 | 2 | 1 | ||||||||||||
| 1 | 3 | 3 | 1 | |||||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
Der binomische Lehrsatz liefert auch die bekannten binomischen Formeln:
Die folgenden Videos sollen die theoretischen Erläuterungen unterstützen:
| Bruchrechnung 2 | Bruchrechnung 3 |
| Binomialkoeffizienten | Binomische Formeln |
| Diese Videos sind Bestandteil des Moodle-Projekts innerhalb der HTW Berlin. | |
3.2 Beispiele
Beispiel 3.2.1
Berechnen Sie den Binomialkoeffizienten .Lösung:
Beispiel 3.3.2
Bestimmen Sie mit Hilfe des binomischen Lehrsatzes!Lösung:
Der folgende Pencast erläutert ausführlich eine weitere Beispielaufgabe:
3.3 Übungen
Die Lösungen zu den hier gestellten Übungen finden Sie im Kapitel "Hinweise und Lösungen zu den Übungen". Zu jeder Übung wird eine Bearbeitungszeit vorgegeben.Übung 3.3.1
Bitte berechnen Sie den Binomialkoeffizienten . Bearbeitungszeit: 3 Minuten
Übung 3.3.2
Bestimmen Sie eine Formel für mit Hilfe des binomischen Lehrsatzes. Bearbeitungszeit: 5 Minuten
Übung 3.3.3
Vereinfachen Sie folgenden Ausdruck so weit wie möglich:
Übung 3.3.4
Vereinfachen Sie den Ausdruck so weit wie möglich:
Übung 3.3.5
Vereinfachen Sie folgenden Ausdruck:
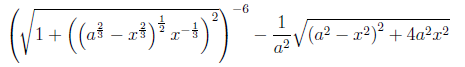
Zum Test
- Startseite
- Einführung
- Inhaltsverzeichnis
-
13 Hinweise und Lösungen zu den Übungen
- 1 Umstellen von Gleichungen
- 2 Potenzen und Wurzeln
- 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
- 4 Polynomdivision
- 7 Lineare Funktionen
- 8 Quadratische Funktionen
- 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
- 10 Exponential- und Logarithmusfunktionen und -gleichungen
- 11 Trigonometrische Funktionen
- 12 Funktionen in Polarkoordinaten
-
14 Hinweise und Lösungen zu den Tests
- 1 Umstellen von Gleichungen
- 2 Potenzen und Wurzeln
- 3 Binomialkoeffizienten, binomische Formeln und binomischer Lehrsatz
- 4 Polynomdivision
- 7 Lineare Funktionen
- 8 Quadratische Funktionen
- 9 Potenz- und Wurzelfunktionen, Wurzelgleichungen
- 10 Exponential- und Logarithmusfunktionen und -gleichungen
- 11 Trigonometrische Funktionen
- 12 Funktionen in Polarkoordinaten


